R-EDA1によるデータ分析 | Rによるデータ分析
R-EDA1によるデータ分析 | Rによるデータ分析
 R-EDA1によるデータ分析 | Rによるデータ分析
R-EDA1によるデータ分析 | Rによるデータ分析
R-EDA1 のリリースノートです。 GitHubの https://github.com/ecodata22/R-EDA1 でバージョン管理しているので、そちらにも更新のコメントは入れていますが、英語ですし、 コードのどこが変わったのかよりも、できることの何が変わったのかに興味がある方の方が多いと思いますので、このページも作っています。
ちなみに、このサイトの更新は、 トップページ や 古い更新履歴 にあります。
これまで欠損値の扱い方については、それぞれのパッケージに任せていました。 パッケージの対応は、大きく3つに分かれていました。 1つめは、ggplotが代表的で、欠損値を「NA」というカテゴリとして処理して、層別の分析ができるようになっています。 2つめは、欠損値のあるサンプルは削除して、先に進むパッケージです。 3つめは、欠損値があれば、エラーが出て、先に進めないパッケージです。
今回、量的変数は、質的変数に変換して進むタイプの方法については、欠損値を「NoData」というカテゴリに変換するようにしました。 量的変数でも、質的変数でも、欠損値なら、「NoData」となります。
変数の類似度の分析では、欠損値もひとつのカテゴリとして、考慮することにしています。
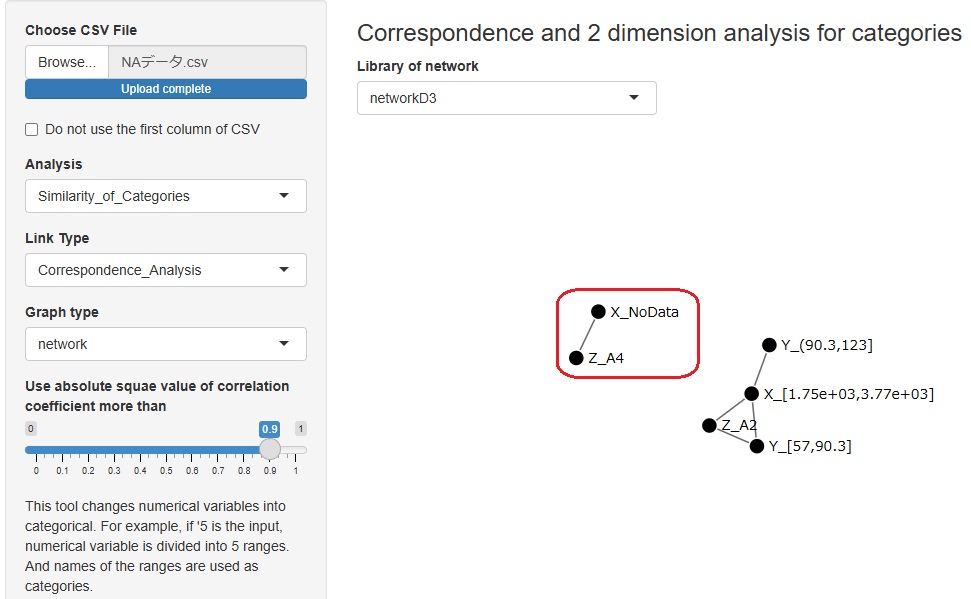
カテゴリの類似度の分析では、もしも欠損値と関係の強いカテゴリがあれば、検出できるようになりました。 例えば、下の例になります。 これは、Xという変数の欠損値(NoData)は、Zという変数の「A4」というカテゴリと組み合わさることが多い事を示しています。
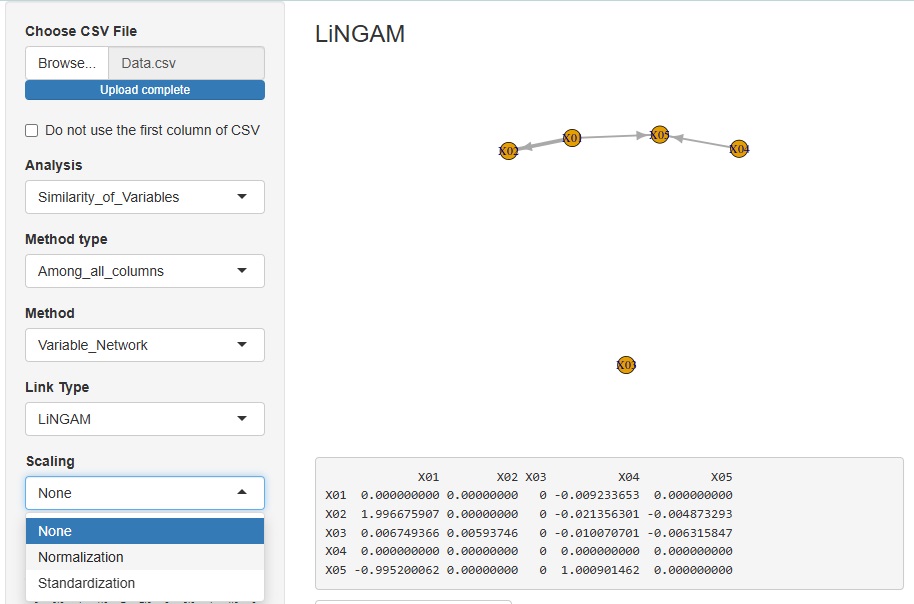
LiNGAM のコードを修正しました。
Rには、「pcalg」というLiNGAMが使えるパッケージがあるのですが、CRANにはないパッケージを参照しているため、Shinyで使えないです。 そのため、R-EDA1では、pcalgの代わりに自作のコードを採用していたのですが、このコードは、結果が不安定で、良くありませんでした。
今回、自作のコードを作り直しました。 限られた事例の範囲ですが、pcalgと同等の性能があることは確認しています。
また、この修正に合わせて、標準化と正規化を前処理として使えるようにもしました。
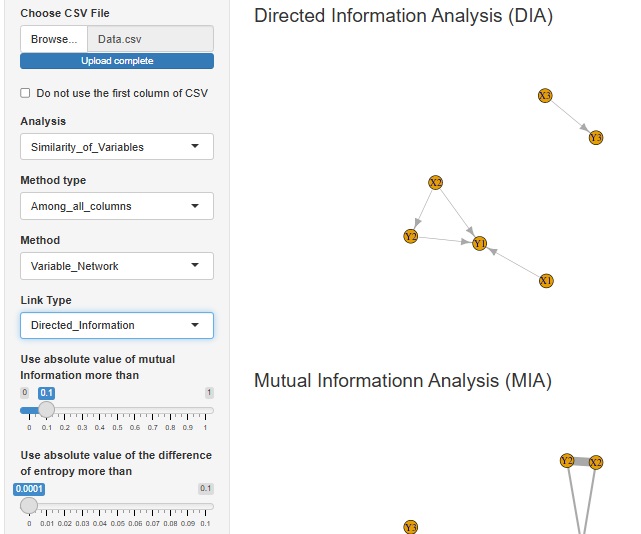
有向情報量分析 (Directed Information Analysis : DIA) の機能を追加しました。
まず、量的変数があれば、質的変数に変換します。
次に、相互情報量を計算して、相互情報量の高い変数の組合せを抽出します。(Mutual Informationn Analysis : MIA)
最後に、相互情報量の高い変数の組合せについては、平均情報量を比べて、矢印の方向を決めます。
ハイブリッド有向相関分析 (Hybrid Directed Correlation Analysis : HDCA) の機能を追加しました。
まず、相関係数と偏相関係数で、矢印の向きを検討するエッジを特定します。 次に、条件付き独立だけで判断できる向きを抽出します。 最後に、条件付き独立では判断できない向きについて、正規化と標準偏差を使って向きを判断します。
条件付き独立をできるだけ使うことで、 LiNGAMでは扱えないデータでも、できるだけ対応します。
また、正規化と標準変数を使うことで、条件付き独立(
ベイジアンネットワーク
)だけでは決まらないパターンに対応します。
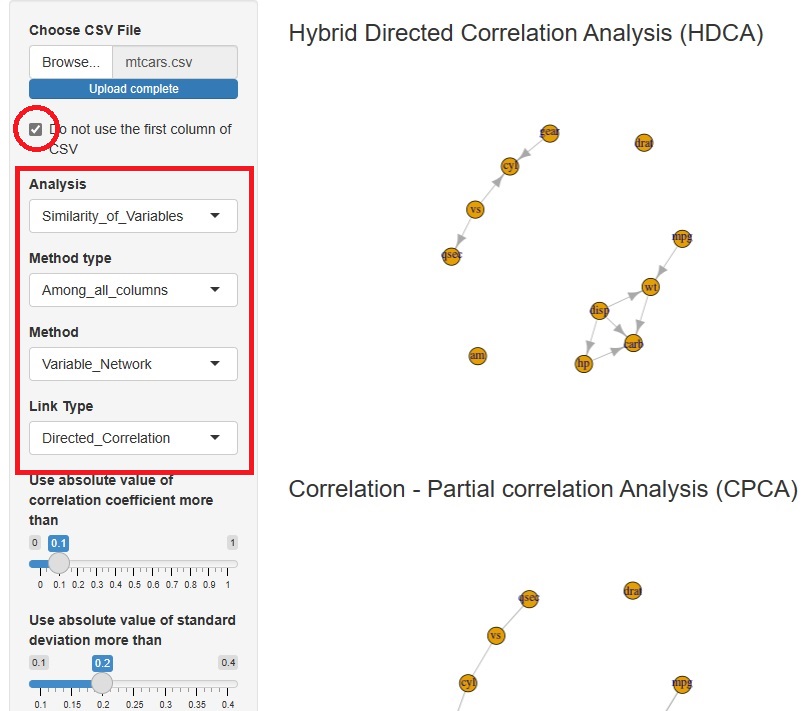
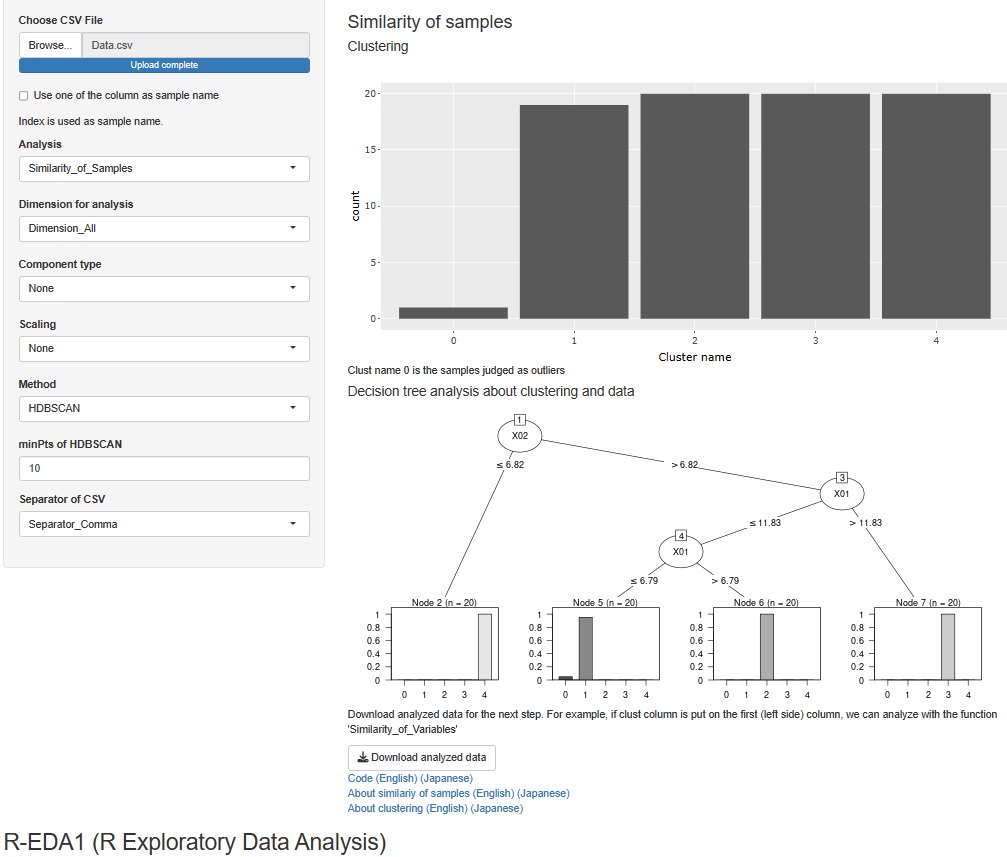
全変数についてのクラスター分析は、階層型、DBSCAN、HDBSCANがありましたが、これに混合分布法を追加しました。
また、全変数についてのクラスター分析をした場合、今までは、元のデータにクラスタリングの結果を追加したデータが、csvファイルで出力できるようになっていただけでしたが、クラスターを目的変数とした決定木分析もできるようにしました。
クラスタリングの原因分析
ができます。
質的変数をダミー変換すると、量的変数の類似度の分析の方法を、カテゴリの類似度の分析の方法として使うことができます。 そのため、変数とカテゴリの分析は、同じところにいれていました。
また、カテゴリの類似度の分析は、アソシエーション分析しかないと思っていたこともあり、カテゴリの類似度の分析だけで、ひとつの柱にはしていませんでした。
しかし、質的変数をダミー変換して、変数の類似度の分析を使うより、量的変数を質的変数に変換して、 質的変数の類似度の分析をしたり、カテゴリの類似度の分析に持ち込む方が、良いことが多いです。 また、コレスポンデンス分析は、カテゴリの類似度の分析です。
そこで、分離させました。
主成分回帰分析 に 個別の因子の寄与率 の分析を追加しました。 4種類の寄与率を使った分析ができるようになりました。
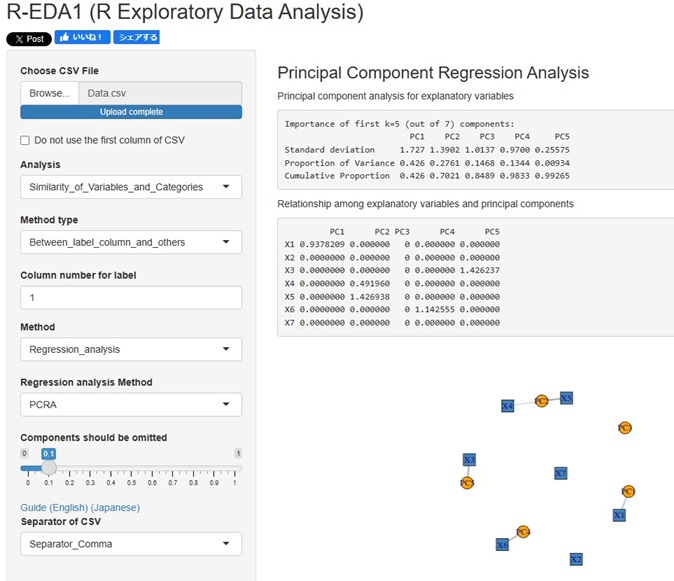
ダミー変換 は、「dummies」と「fastDummies」の2つを使い分けていたのですが、全部、「fastDummies」に統一しました。
「dummies」がCRANから削除されてしまい、使えなくなったのが理由です。
いずれのライブラリも、量的変数と質的変数が混ざっている時に、質的変数だけを変換してくれるところが便利です。
ただ、「fastDummies」には、「全部が量的変数で、変換対象がひとつもないとエラーになる」という弱点があります。 そこで、変換の前に、全部の変数をチェックして、変換対象がなければ、このライブラリは使わないようにしました。 そのため、従来、1行で済んでいたところが、5行に増えています。
比例分散の回帰分析 ができるようにしました。 上側の散布図には、 比例分散の予測区間 が出ます。 また、下側のヒストグラムは、比例分散の元になっている「Y/X」の分布がわかるようにしてあります。
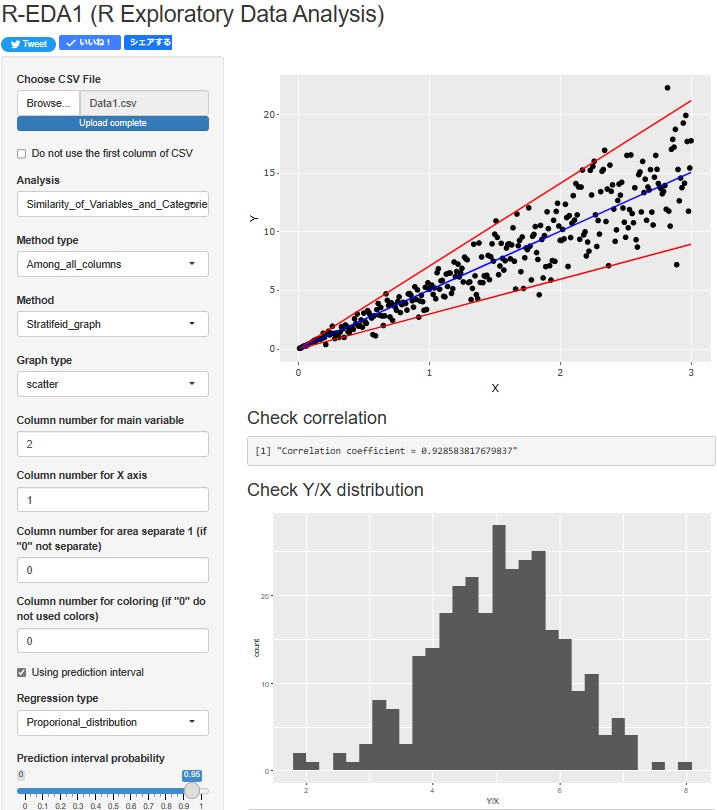
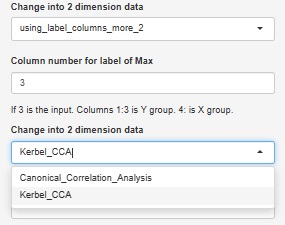
正準相関分析で高次元を2次元に圧縮 の分析の機能を追加しました。
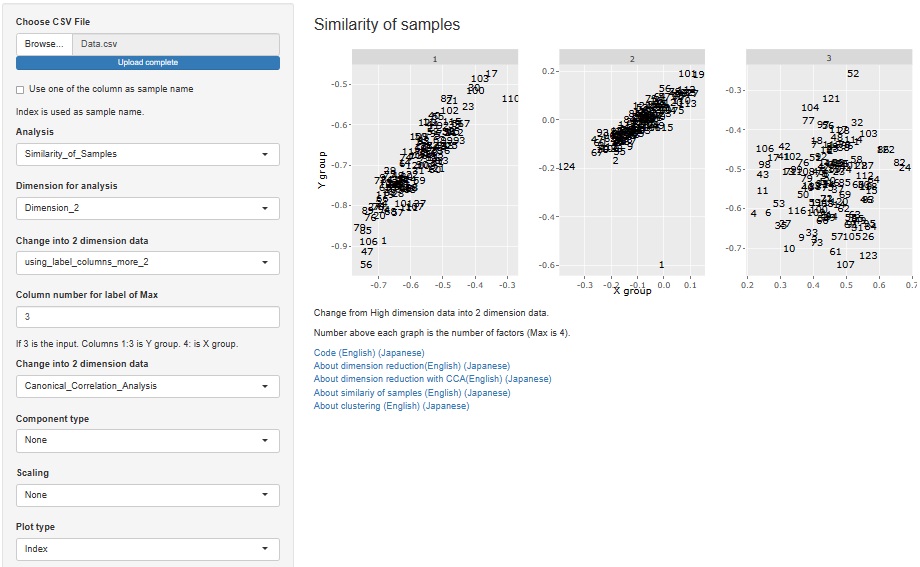
Rによる正準相関分析
には、カーネル法による非線形の正準相関分析もありますが、これも使えるようになっています。
回帰分析系で高次元を2次元に圧縮して可視化 と 残差の外れ値 の分析の機能を追加しました。
回帰分析系の方法としては、 回帰分析 、 モデル木 、 サポートベクター回帰 の3種類が使えるようになっています。
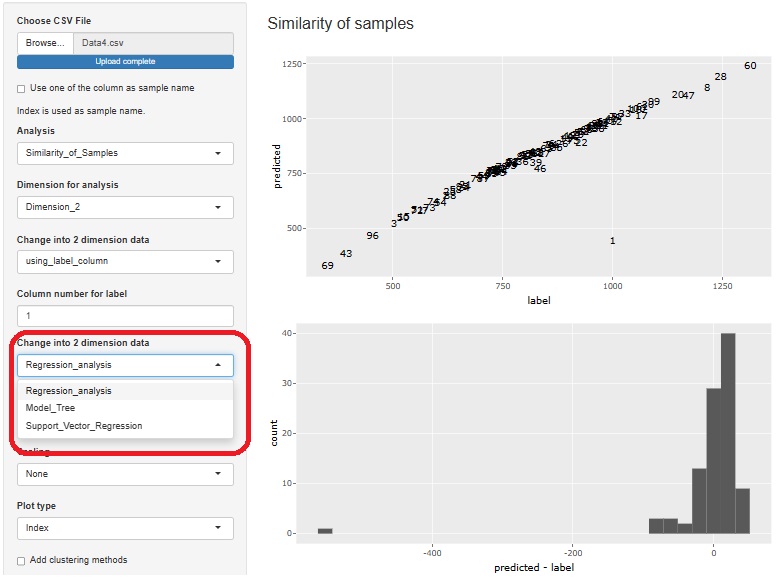
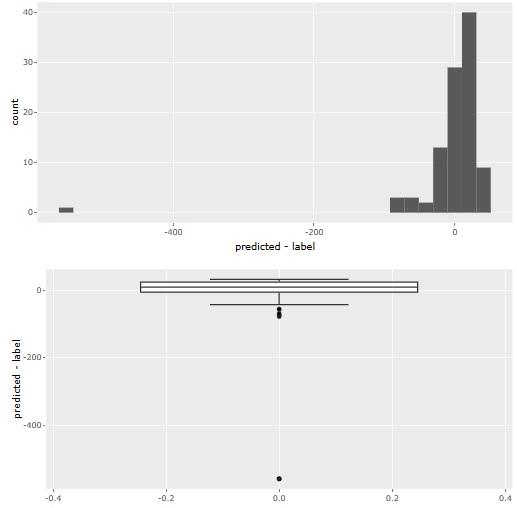
残差の分析は、ヒストグラムと箱ひげ図の両方が出ます。
ヒストグラムだと、サンプル数が非常に大きくなった時に、外れ値が見えにくくなるので、そういう場合は箱ひげ図の方が良いです。
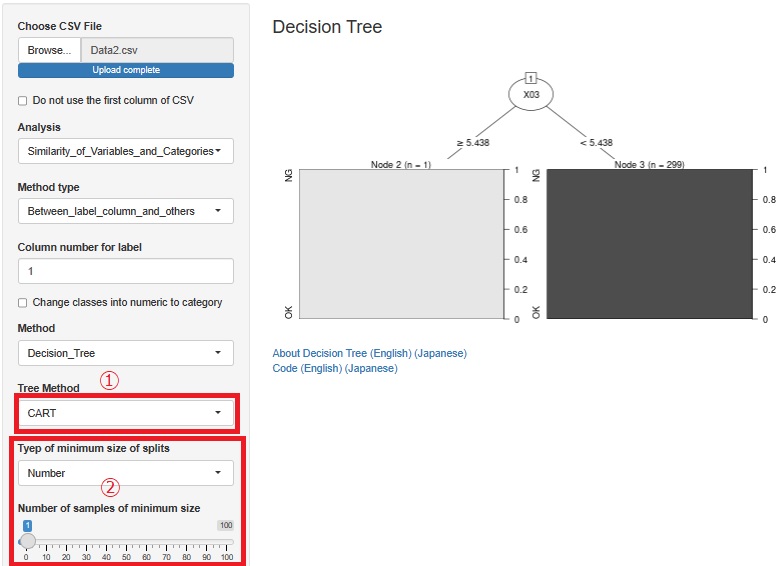
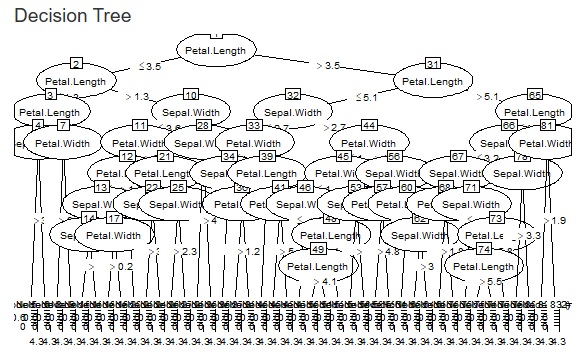
決定木 のCARTを追加しました。図の①のところです。 C5.0があるので、CARTは不要と思っていたのですが、C5.0は分岐のルールが厳しめのようなので、CARTも入れることにしました。
また、 Rによる個々のサンプルの因果推論 のページの使い方ができるように、最小サンプル数も調整できるようにしました。 今までは、最小サンプル数の割合(Ratio)だけが調整できるようにしていたのですが、具体的なサンプル数の指定もできるようになりました。図の②のところです。
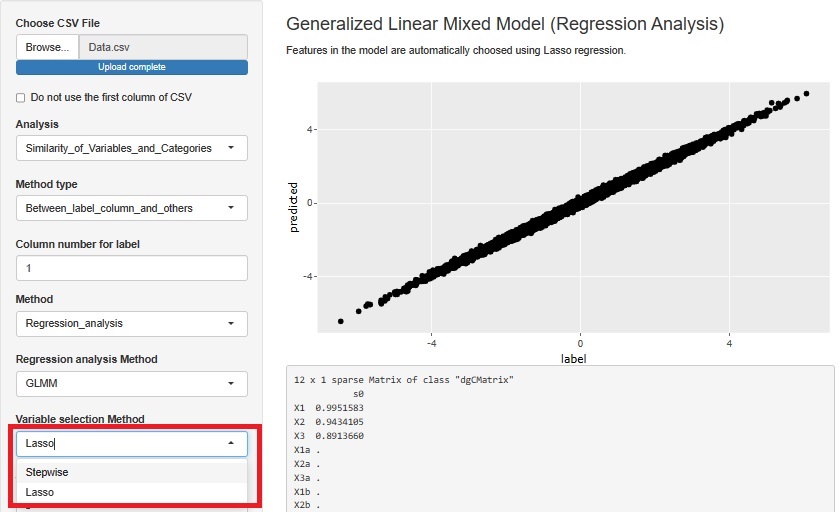
Rによる変数の重要度の分析 にある ラッソ回帰 を追加しました。
「 ラッソ回帰 の機能を追加」というよりも、 一般化線形モデル の変数の選択の方法が、今までのステップワイズ法に加えて、ラッソ回帰が入った、位置付けにしています。
出力として出て来る散布図は、予測値と実測値の関係が分かるようにしています。 直線状なら、精度が高いことになります。 下の法にある変数と数値のリストは、標準偏回帰係数の計算結果になっています。 これによって、変数の重要度が評価できます。
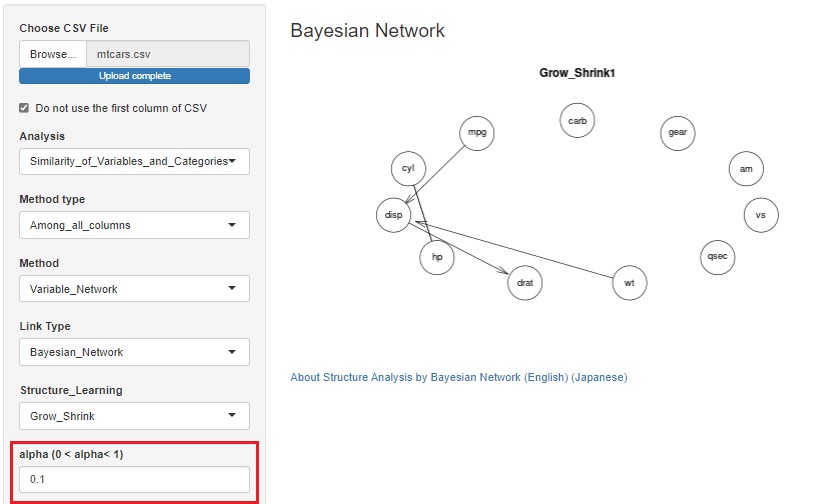
Rによるベイジアンネットワーク にもありますが、ベイジアンネットワークのいくつかのアルゴリズムは、αを使って変数の関係の有無を判定します。
今までは、デフォルト値(0.05)しか使えなかったのですが、変更できるようにしました。
サンプル数が多い時は、これを小さくした方が、意味のある情報を見つけやすくなります。
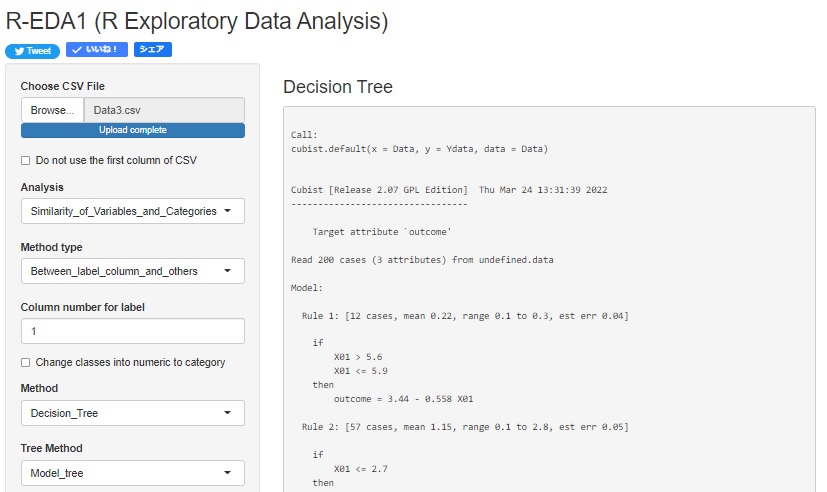
モデル木 を追加しました。 一般的な回帰木は、グループ内は予測値が一定のため、予測値の精度を上げようとすると複雑過ぎて考察ができないモデルになる弱点がありました。 モデル木は、グループ内は回帰式を使うため、シンプルなモデルを作りやすくなります。
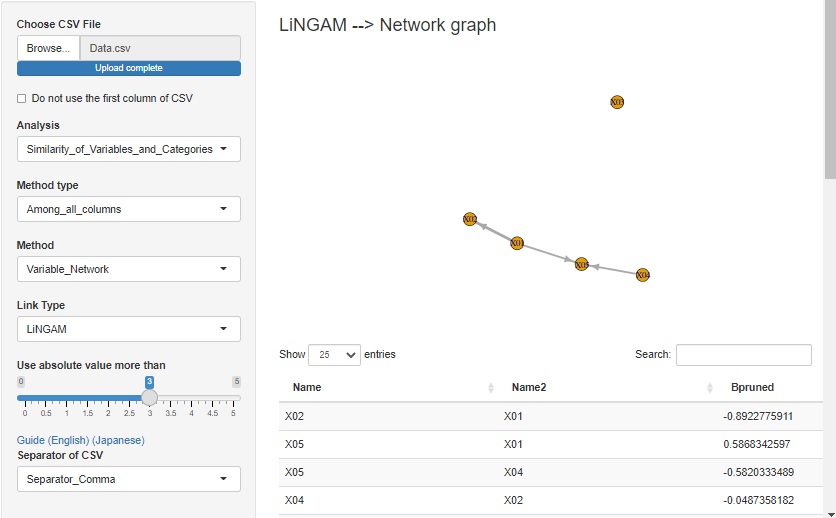
変数の相関関係をネットワークグラフで見る方法のひとつに LiNGAM を追加しました。
誤差が正規分布以外で、変数が パス解析 の時の構造を持っている時に、その構造をあぶり出すことができます。
なお、LiNGAMが使えるRのライブラリにpcalgがありますが、pcalgは、shinyのサーバではエラーが出て使えないため、 筆者が自作したコードを使っています。 コードは、 RによるLiNGAM にあります。
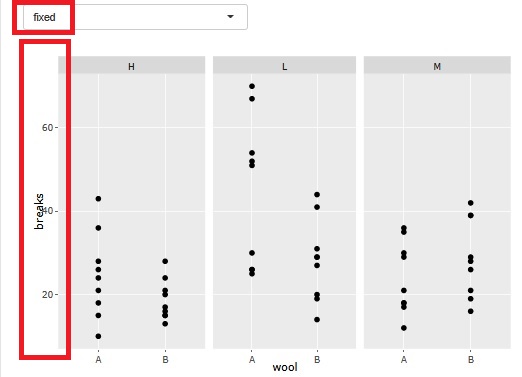
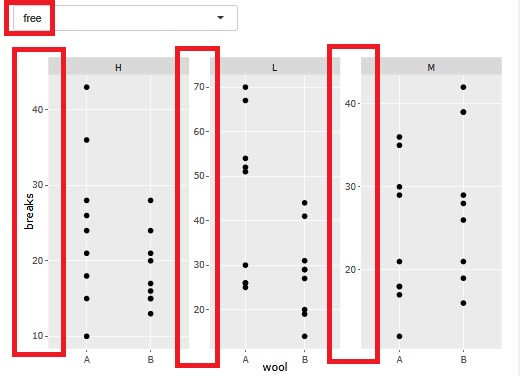
層別の分析をする時に、グラフを層別で分割できる機能があります。 このグラフの時に、今までは、グラフ毎にプロットが見渡せるように軸の範囲が違っていました。
データマイニング のような分析の時には、小さな領域で起きていることを拡大して見る目的では良かったのですが、 全体的な位置付けを見たい時には、わかりにくくなっていました。
そこで、軸の範囲を合わせるかどうかは、選べるようにしました。
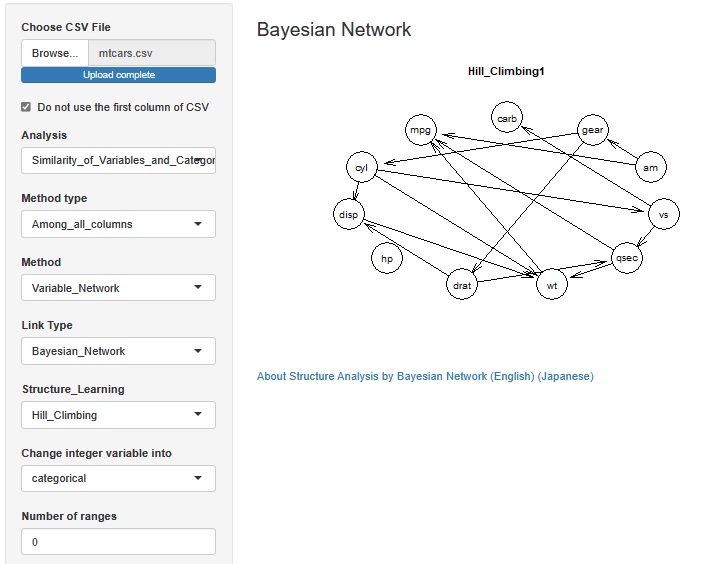
ベイジアンネットワークによるデータの構造解析 では、整数の変数は、質的変数として扱うか、量的変数として扱うのかを選べるようにしました。
一般的な量的変数では、質的変数として扱う時に、区間で区切る方法を使いますが、 この機能で整数を質的変数として扱う時は、例えば、「1、2、5」という3つの整数があれば、これらの3つがそれぞれ質的変数として扱われます。
整数で表されている変数が原因系の変数の時は、ベイジアンネットワークでは、矢印の元の方に質的変数を置くので、
思ったような矢印になりやすくなります。
有効次元数 の分析が一例ですが、距離行列をスタートにする分析方法があります。
この方法は、R-EDA1では 多次元尺度構成法 だけを使えるようにしていたのですが、t-SNE、UMAP、階層型クラスター分析でもできるようにしました。
t-SNE
t-SNEの場合は、次元数は3が最大値です。
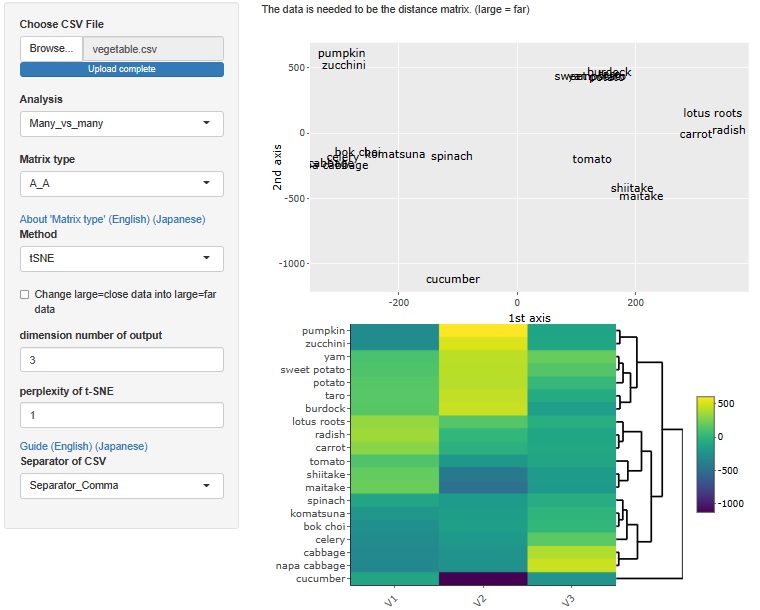
UMAP
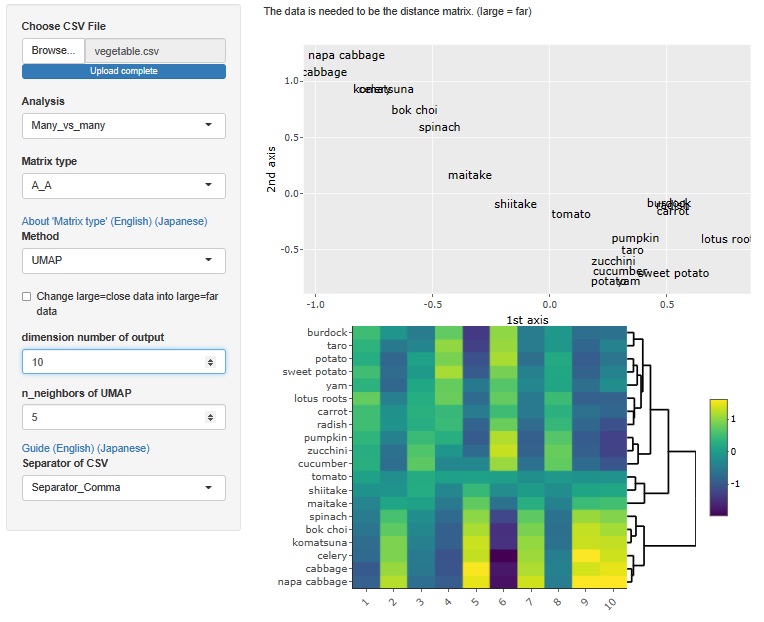
UMAPの場合は、次元数はサンプルの数が最大値です。
ただ、ソフトとしては、大きな次元数でも分析できるようにしていますが、その結果の物理的な考察の仕方が多次元尺度構成法の時のようにはできず、
筆者としては使い道がわからないです。
階層型クラスター分析
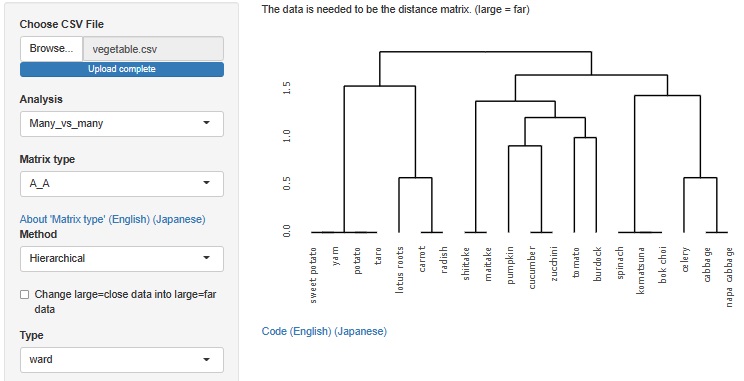
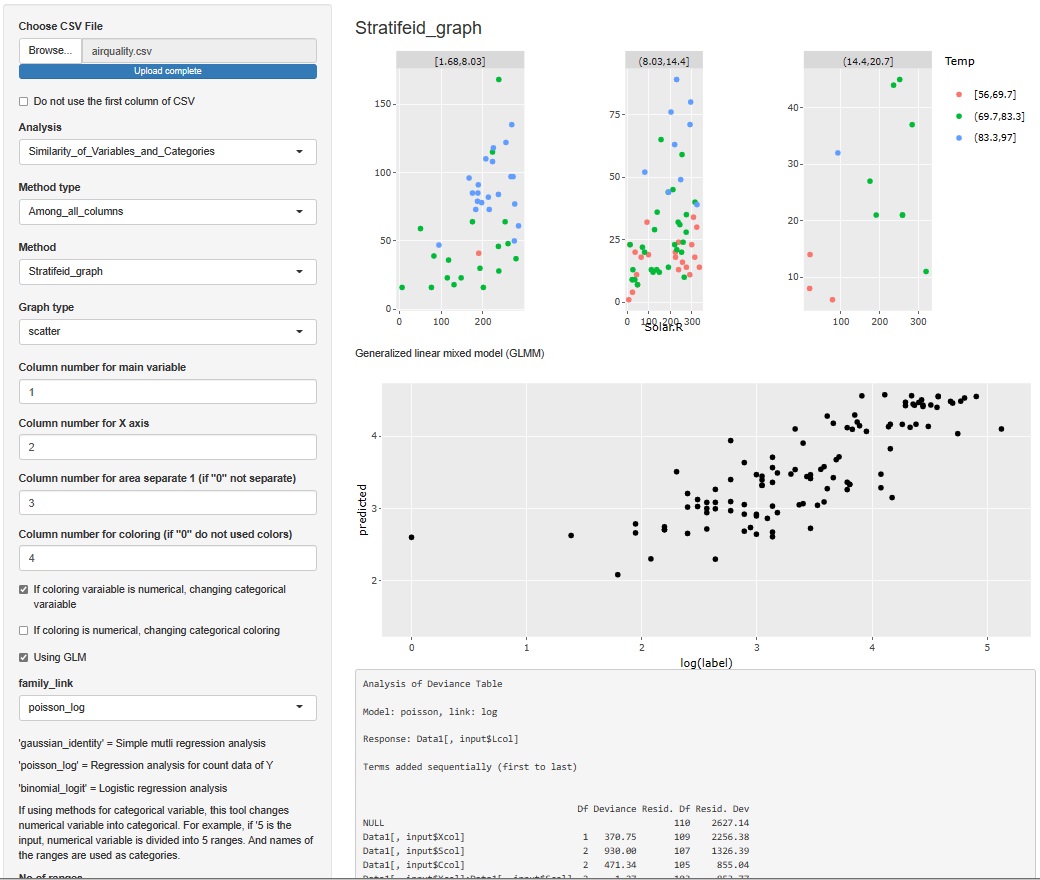
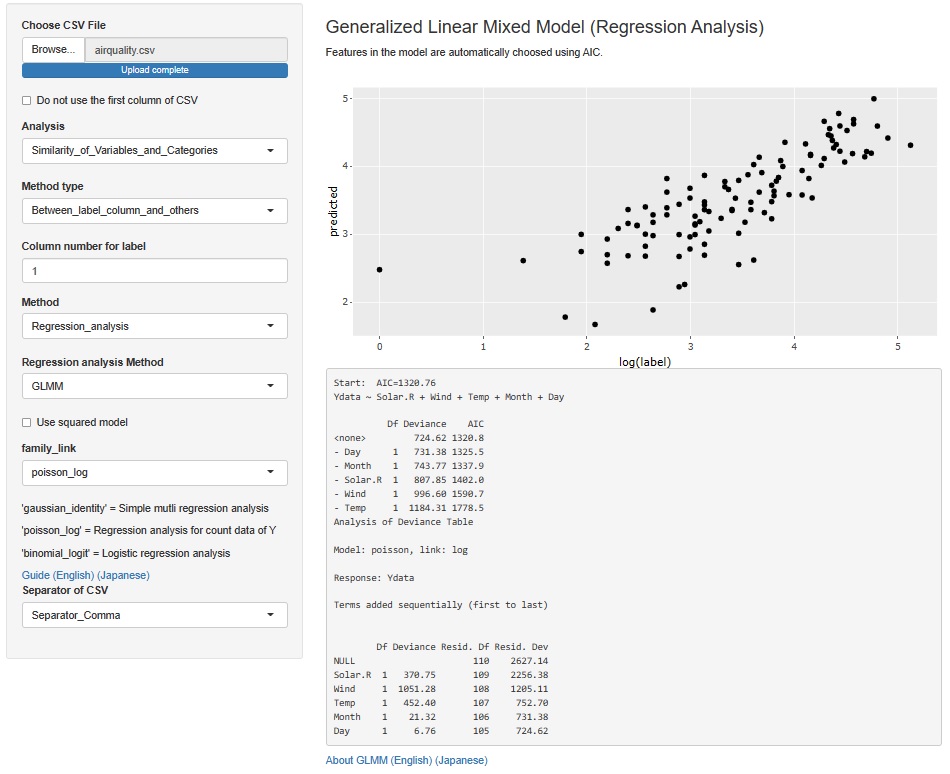
一般化線形混合モデル の結果は、テキストだけだったのですが、ラベルの予測値をY軸、実測値をX軸にしたグラフも出力するようにしました。 R2やAICなどの指標で見るよりも、モデルの出来栄えがわかりやすいです。
一般化線形混合モデル(GLMM)は、2つの場所に入っていますが、両方にこの機能を追加しています。
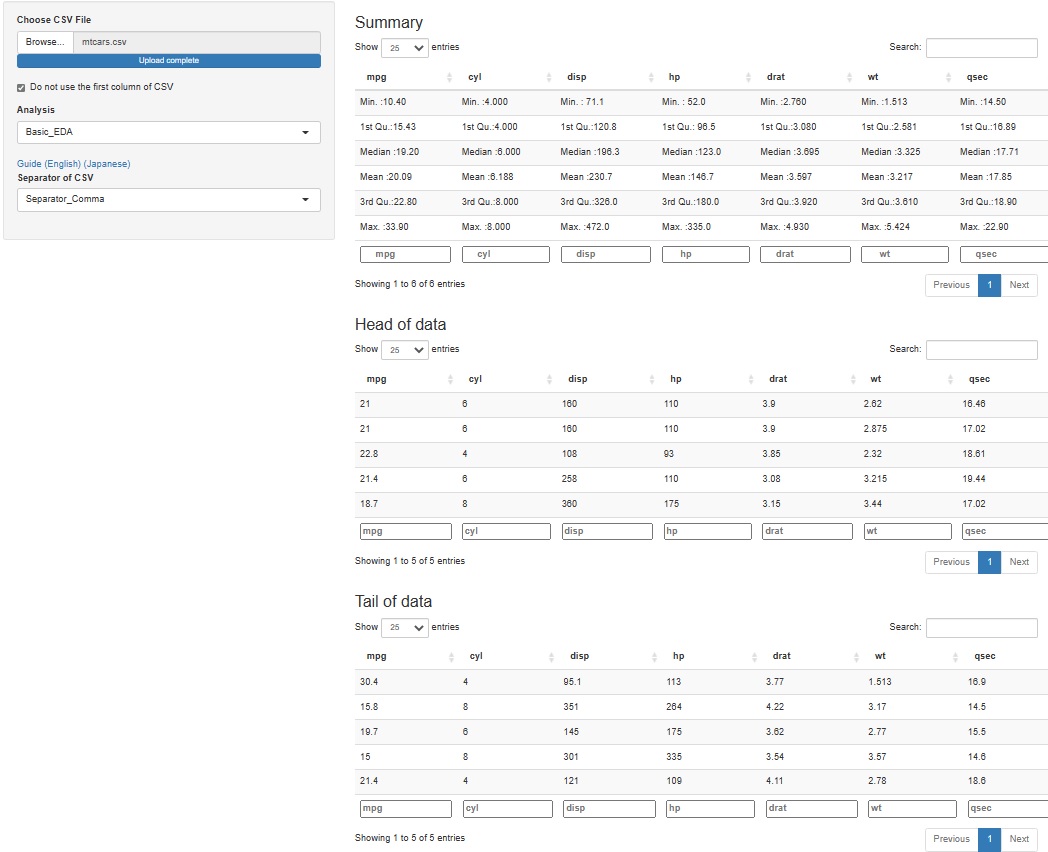
グラフにしたり、計算をするとわからなくなるのですが、 データ分析をする時は、生データ(分析対象のデータ)の具体的な値がどうなっているのかを確認すると、 良いことがあります。 何かの理論を使わなくても、データを見ただけで「これは変だ」とわかることもあります。
全部見る機能を付けるのは大変なので、さしあたって、一番上(Head)と一番下(Tail)の5行ずつを確認できるようにしました。
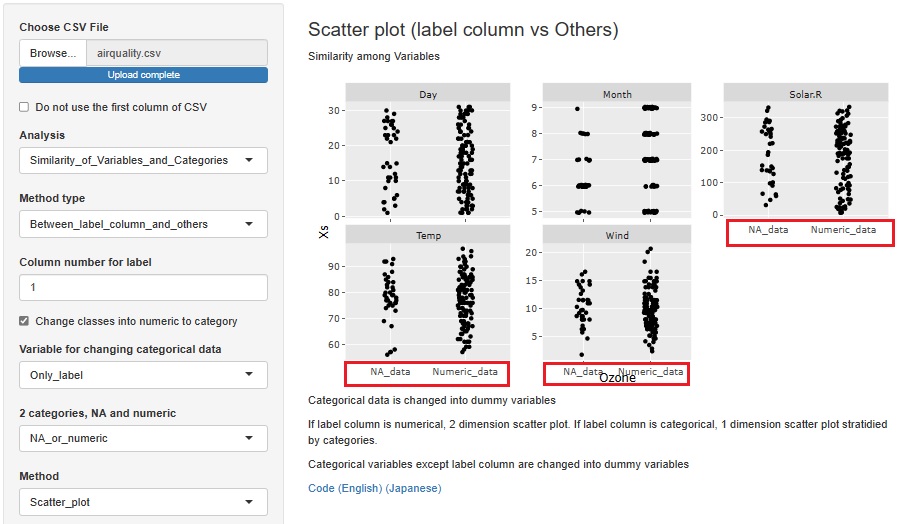
欠損値を含む量的変数を目的変数に選んだ時に、 欠損値を「NA_data」、欠損値以外を「Numeric_data」という名前の質的変数に変換する機能を追加しました。
欠損値が欠損している理由を、他の変数との関係から調べられます。 また、他の変数と何も関係がなさそうな場合は、「欠損はランダムに発生している」という考察もできます。
まず、横軸に目的変数にして、縦軸をすべての他の変数にして、層別の1次元散布図を作る例です。
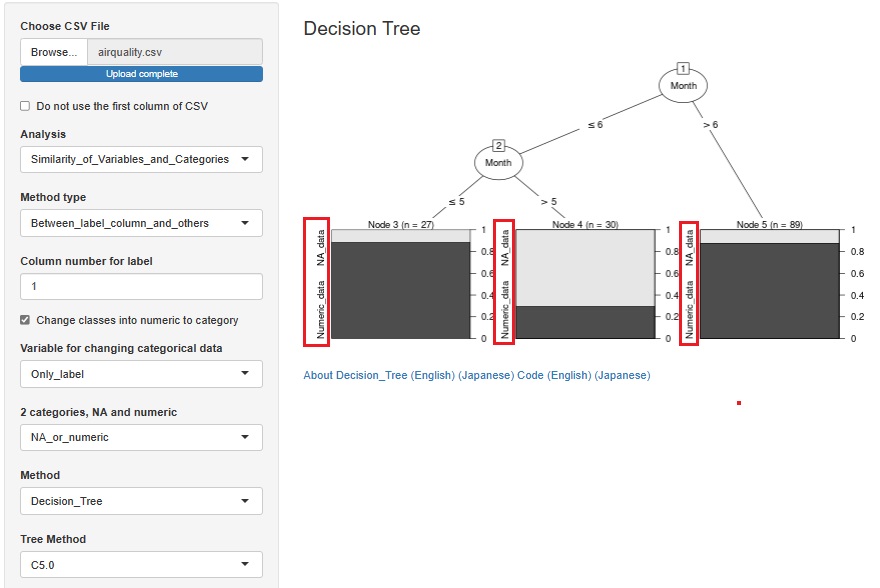
決定木の例です。
MT法の例です。
MT法の場合は、単位空間を欠損していないサンプルにしています。
「0」が欠損値ではないサンプルで、「1」が欠損値のサンプルです。
欠損している理由がいろいろある場合は、決定木よりもMT法の方が良いです。
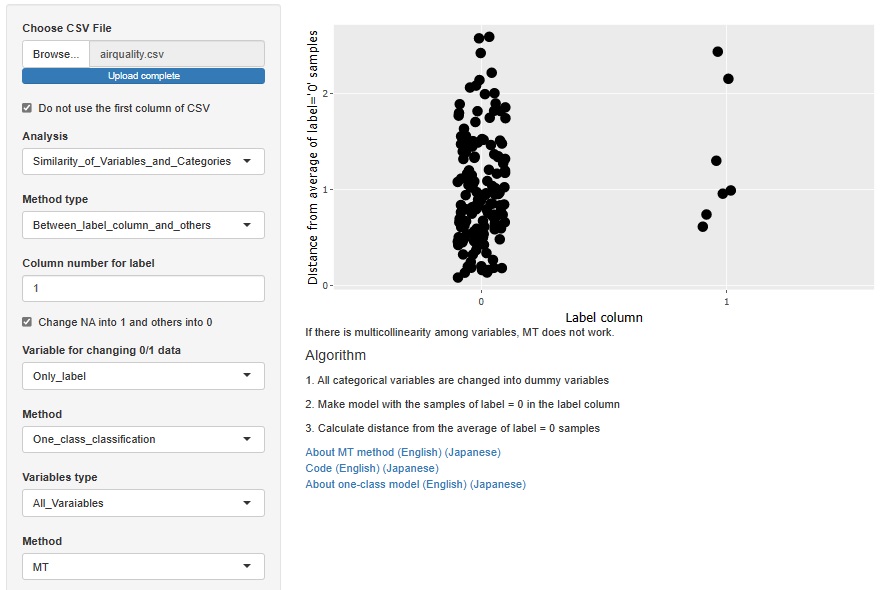
主成分に標準化や正規化 の技を3つの手法で使えるようにしました。
高次元を2次元に圧縮して可視化
の方法を使う時に、上記の方法を単独や、組合せて使えるようにしてあります。
組み合わせた場合は、主成分分析が先に処理されます。
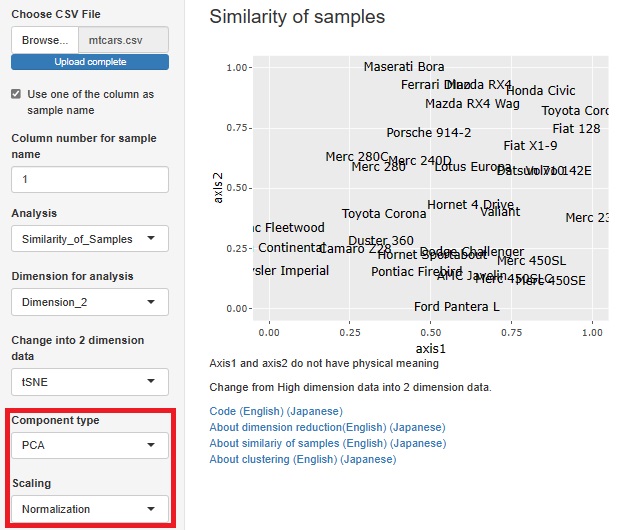
1クラス最小距離法
でも、組合せられます。
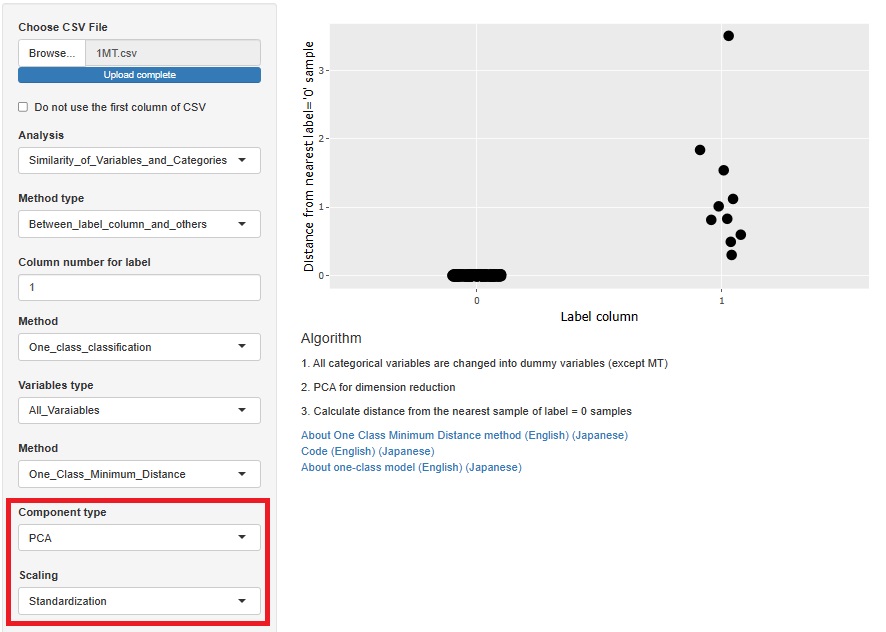
時系列解析
でも、組合せられます。
時系列解析
では、主成分分析(PCA)だけでなく、
独立成分分析(ICA)や
因子分析(Factor_analysis)とも組合せられます。
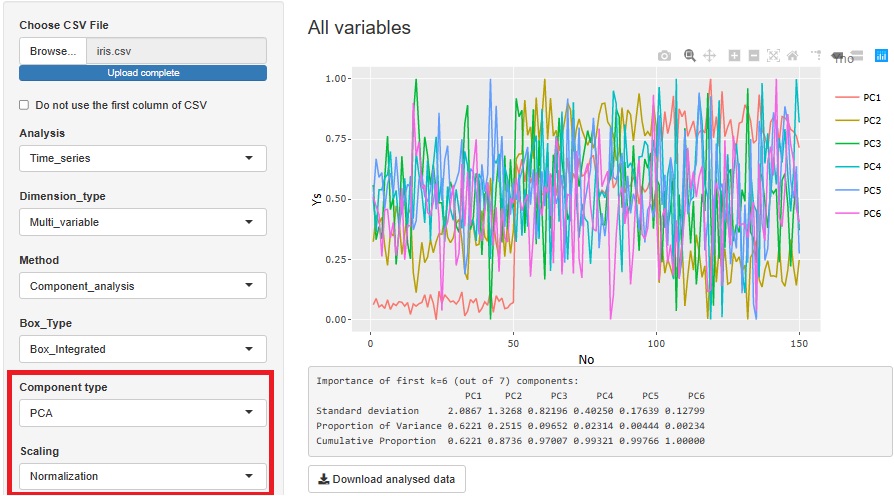
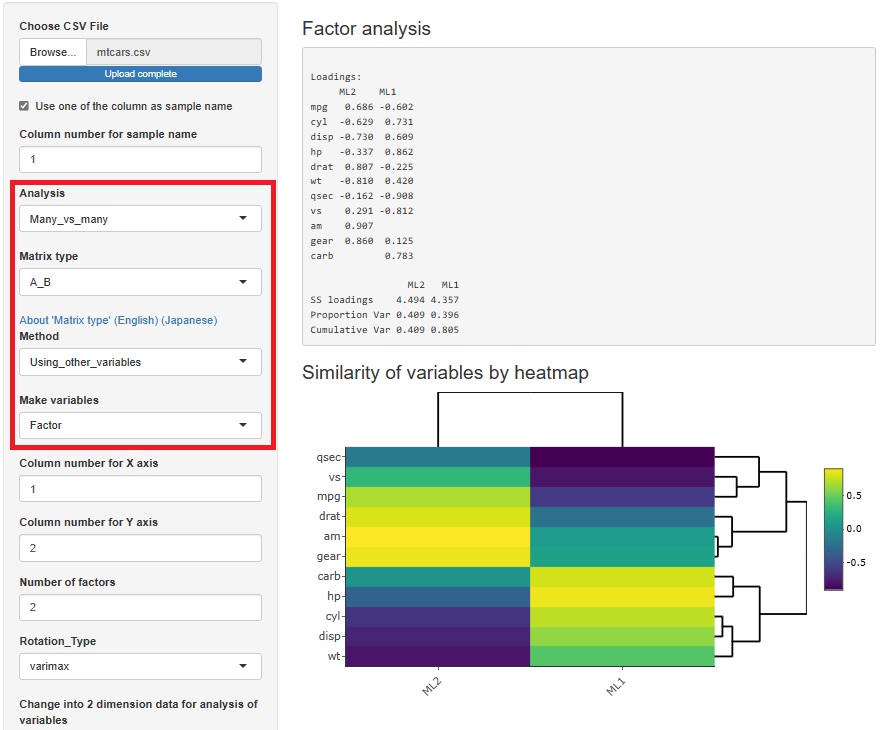
因子分析を、サンプルの類似度の分析から、多対多の分析に引越しました。
サンプルの類似度の分析の方法は、基本的に変数とサンプルの関係は見ないのですが、この点が、ここに配置した他の方法と合わないので、
より適切な場所に移動しました。
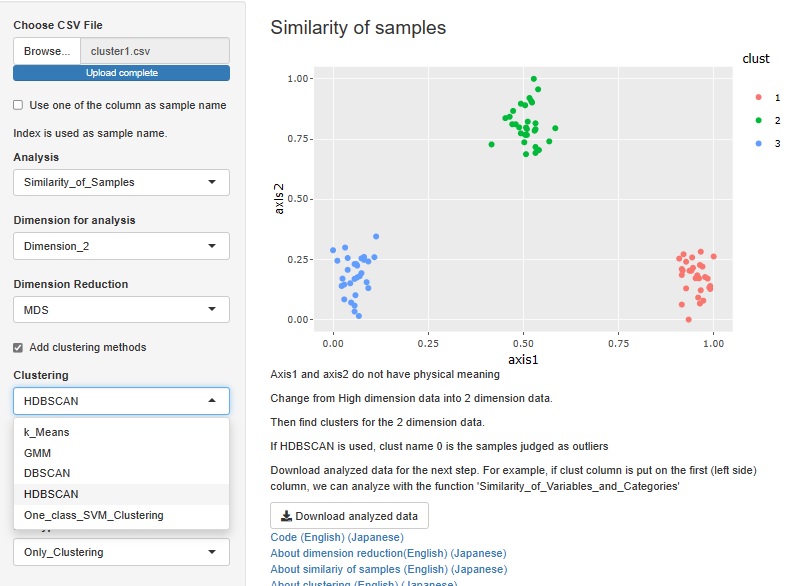
HDBSCANを追加しました。 DBSCANと似ていますが、密度の差があるクラスタがある時に、うまく分けてくれるようになっています。
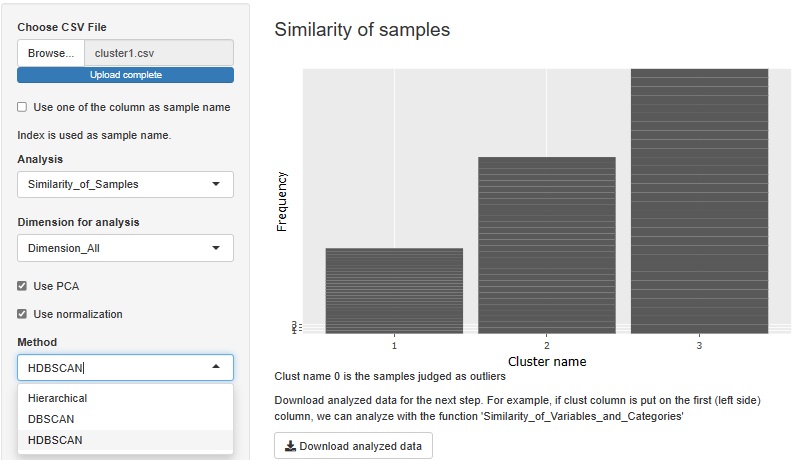
MDS(多次元尺度構成法)とt-SNEが選べるようになっている所に、「UMAP」も選べるようにしました。
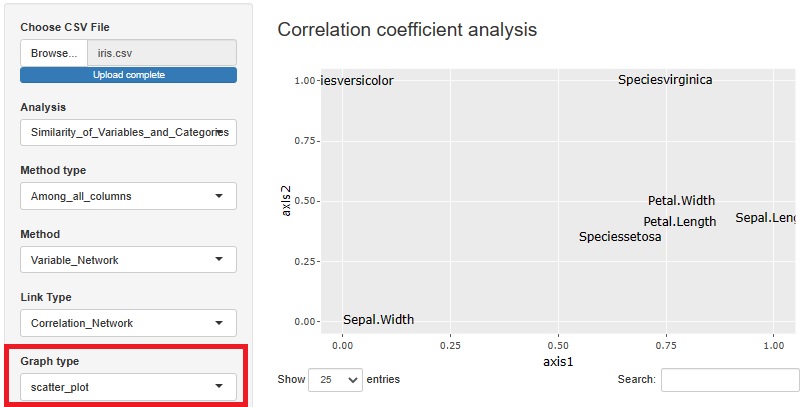
相関係数、グラフィカルラスー、クラメールの連関係数をネットワークグラフで見る方法を入れていましたが、 グラフは散布図にもなるようにしました。
見方はネットワークグラフと似ていて、位置が近い変数同士は係数も高いです。
ネットワークグラフだと「AとBは近い。AとCは近い。BとCはすごく遠い」という場合に、リンクの有無で簡単に表現できるのですが、 散布図だと、「BとCはすごく遠い」ということが表せません。 そういう弱点はあるのですが、散布図はグラフが軽いので、その点はネットワークグラフよりも良いです。

クラスター分析をする時に、前処理として正規化を選べるようにしていたのですが、 正規化の前に主成分分析(PCA)をして、主成分を変数として使えるようにもしました。 正規化をする・しないと、主成分分析をする・しない、で4通りの組合せができます。 どういう多次元データで、どういう風に見たいのかで選べるようになっています。
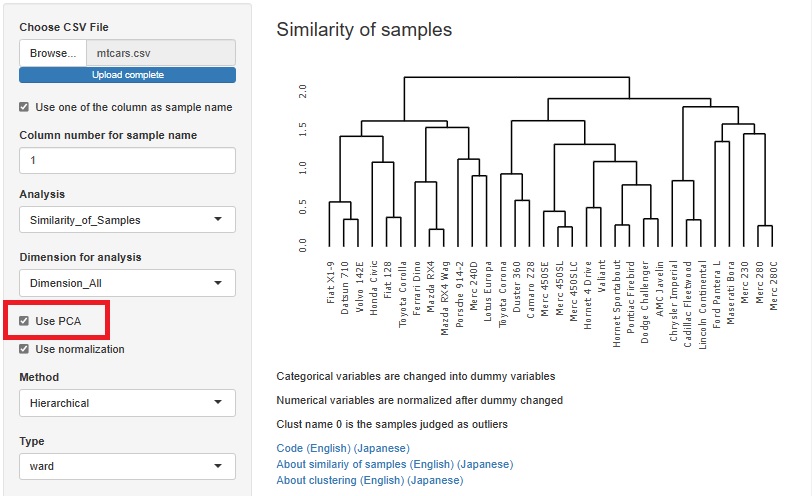
1クラスの手法は、変数全部でモデルを作って分析するものと、1~3個の変数の全部の組合せでモデルを作って、組合せの違いを分析するものがあり、一緒になっていたのですが、分割しました、
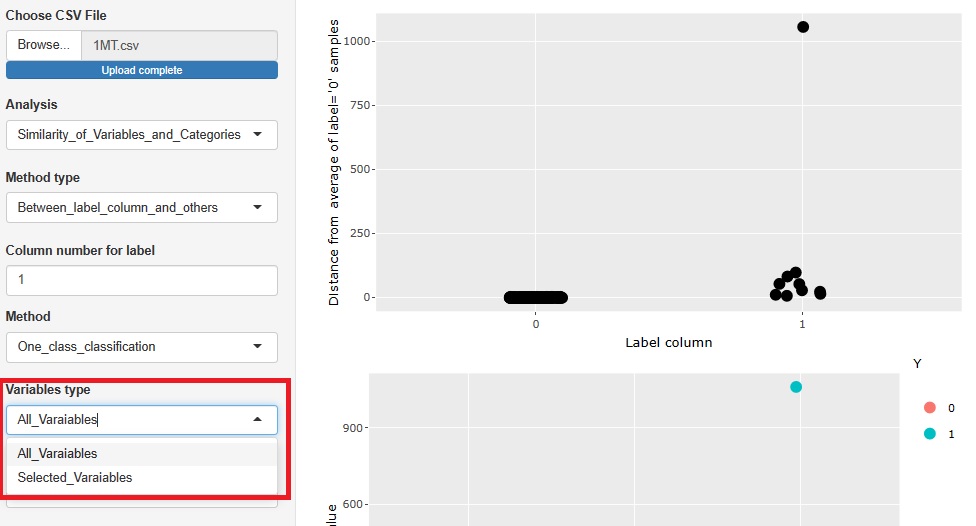
画面スクロールを行ったり来たりする必要があったので、 手法の選択にラジオボタンを使っていたところは、すべてセレクトボックスに変えました。
画面スクロールがゼロにはなりませんが、かなり改善しました。
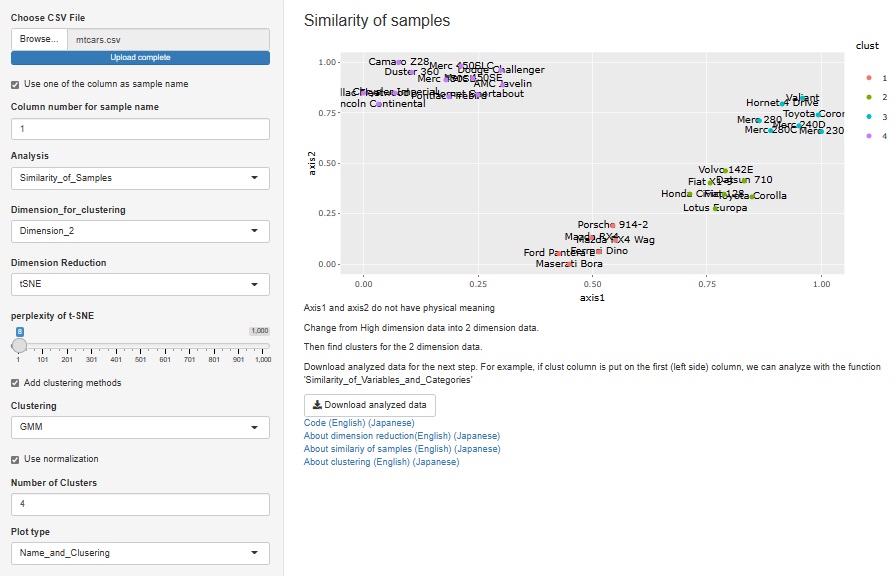
クラスター分析をする時は、必ず正規化を前処理として行うようになっていたのですが、 正規化するかどうかは選べるようにしました。
単位の異なる変数が混ざっている場合は正規化が必要ですが、 データの元々の値の大きさが重要な場合は正規化をするとそれが見えなくなるので、正規化はしない方が良いです。
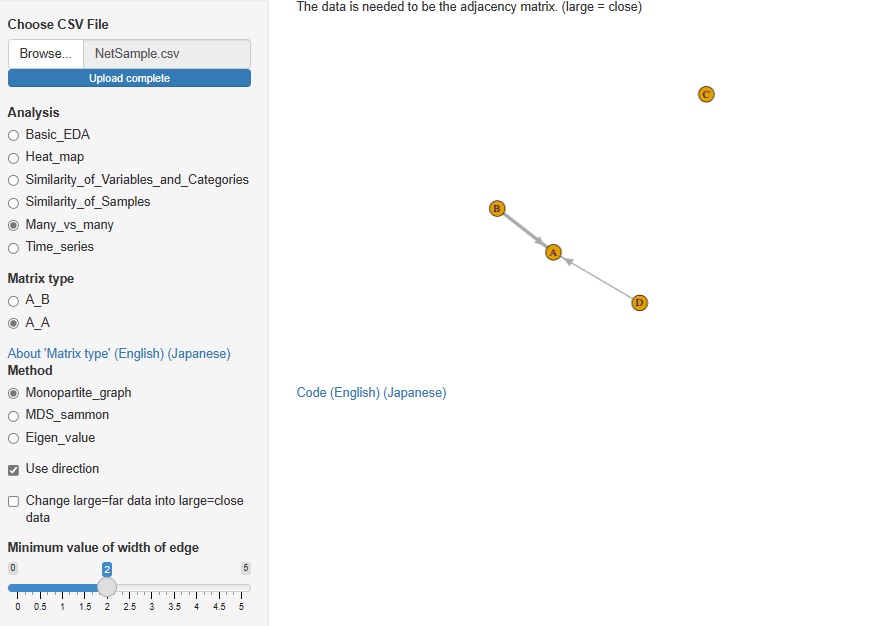
多対多の分析 の内、 A-B型の分析 については、 行と列の項目の、項目同士の類似度の分析 に入っている方法を、R-EDA1に入れていたのですが、 今回、 A-A型の分析 を追加しました。
隣接行列をスタートにした時のネットワークグラフによる分析、
距離行列をスタートにした時の多次元尺度構成法(MDS)による分析、
相関行列や一対評価のデータをスタートにした時の固有値、固有ベクトルによる分析ができるようにしてあります。
リコメンドや、テキストデータの分析方法として、行と列の項目のクラスター分析がよく行われているようです。 SVD (Singular Value Decomposition:特異値分解)はそのひとつですが、R-EDA1に追加しました。
下のグラフの赤い字は、各列の名前(変数の名前)で、青い字は、各行の名前(サンプルの名前)です。 変数に「温度」と「湿度」がある場合など、変数毎に物理的な意味が異なるデータでは、こんな分析はできません。 しかし、すべての変数がカウントデータ(数えて得られる数。頻度など)だったり、点数だったりして、物理的に同じ意味の場合は、 この方法が使えます。
SVDと、コレスポンデンス分析を使い分けられるようにしてあります。 SVDは、負の値があっても扱えますが、コレスポンデンス分析は正の値しか扱えません。
SVDやコレスポンデンス分析で生成するデータは、多次元になりますが、
MDS(多次元尺度構成法)やt-SNEを使って、2次元の散布図で見えるようにしてあります。
「コレスポンデンス分析・SVD」の片方と、「MDS・t-SNE」の片方を選べるので、2×2=4通りの組合せができるようにしています。
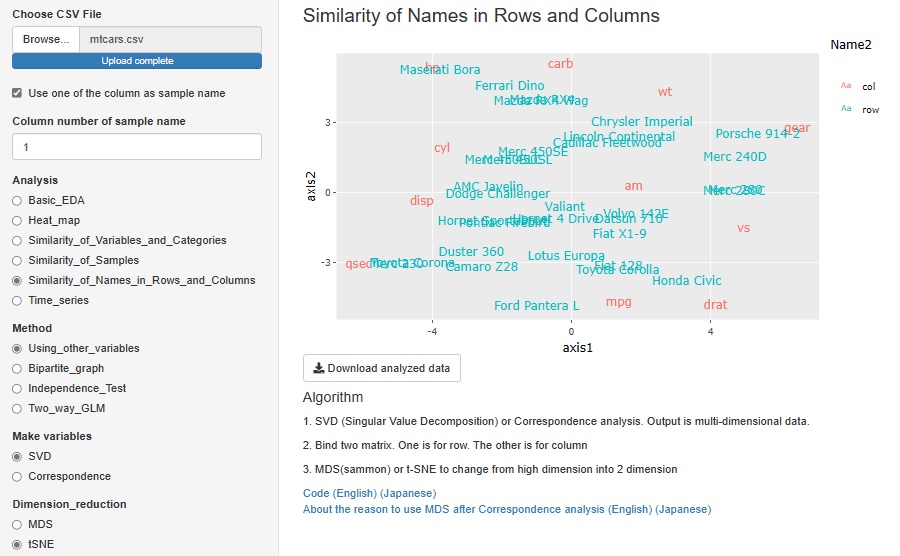
この機能は、もともとコレスポンデンス分析とMDSの組合せの一択でした。 今回、SVDとt-SNEを増やすことで、4通りの方法ができるようになりました。
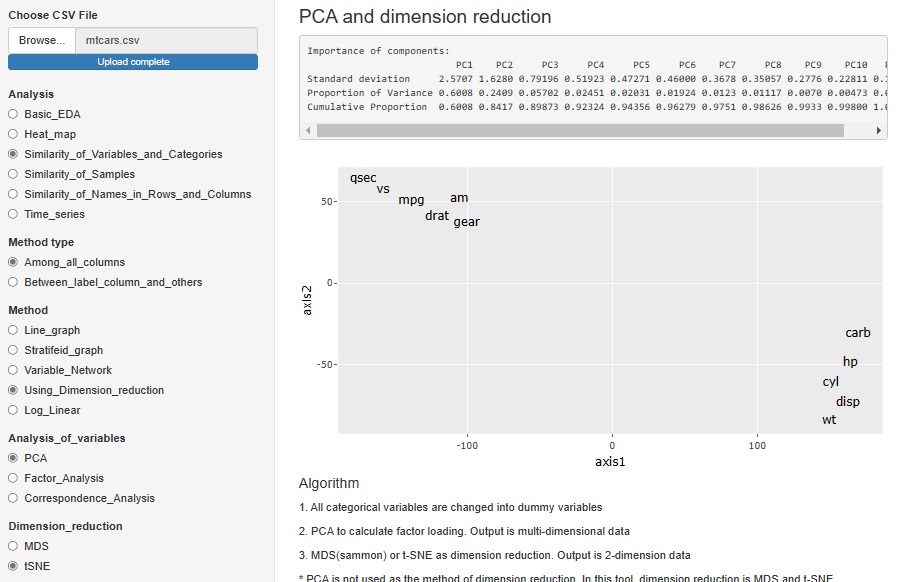
PCA(主成分分析)、Factor analysis(因子分析)、Correspondence analysis(コレスポンデンス分析)で、変数の類似性を分析する方法は、
多次元を2次元で見る方法として、MDSだけを採用していましたが、t-SNEでもできるようにしました。
「Analysis」に「Time series(時系列)」を加えました。
今までは時系列解析をやろうとすると、ヒートマップや、折れ線グラフしかなかったのですが、だいぶ増えています。
全体に共通することとして、「2021/10/19 13:30」のような時刻のデータは使わないです。 時刻のデータは、表記の仕方が様々で全部に対応するツールは作りきれないためです。 その代わり、データは「1分おき」などの等間隔の時間で収集されたことを想定しているので、 データの個数で「時間」の分析ができるようにしてます。 1分間隔の場合、「n = 12」は「12分」です。
「Multi_variable(多変量)」の中の「Stratifeid_graph(層別グラフ)」は、注目したい変数の折れ線グラフです。
他の変数を使って色分けしたり、グラフを分割することができます。
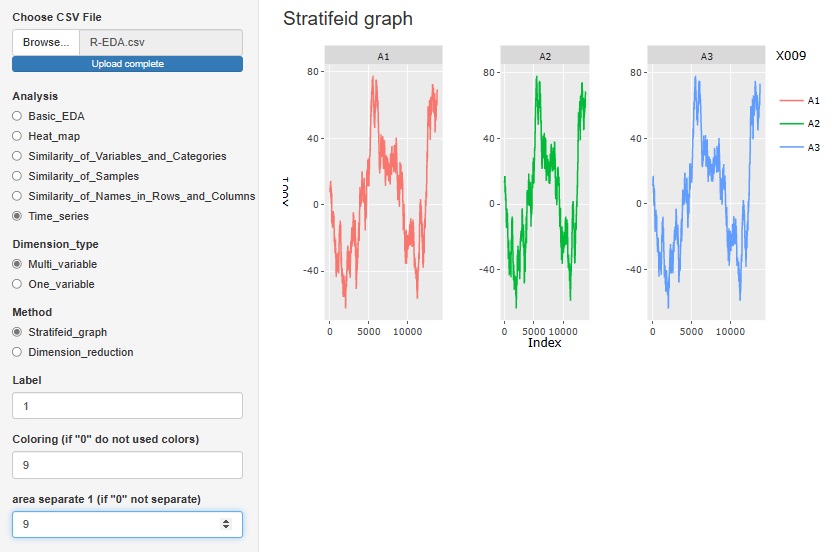
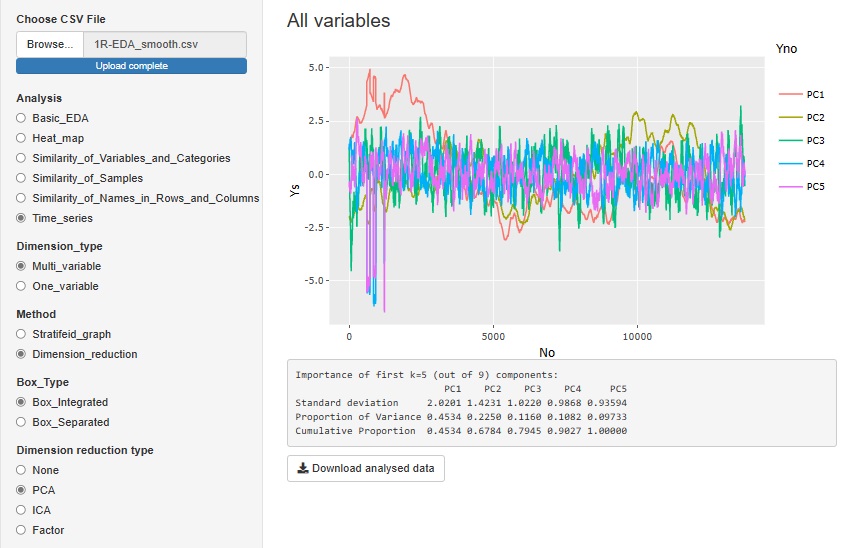
「Multi_variable(多変量)」の中の「Dimension_reduction(次元削減)」は、次元削減の方法で変換した変数の全部を見るためのグラフです。
下図は、「PCA(主成分分析)」を選んだ場合です。
「ICA(独立成分分析)」や「Factor(因子分析)」でもできます。
「None」を選ぶと、元の多変量全部を一緒に見るグラフになります。
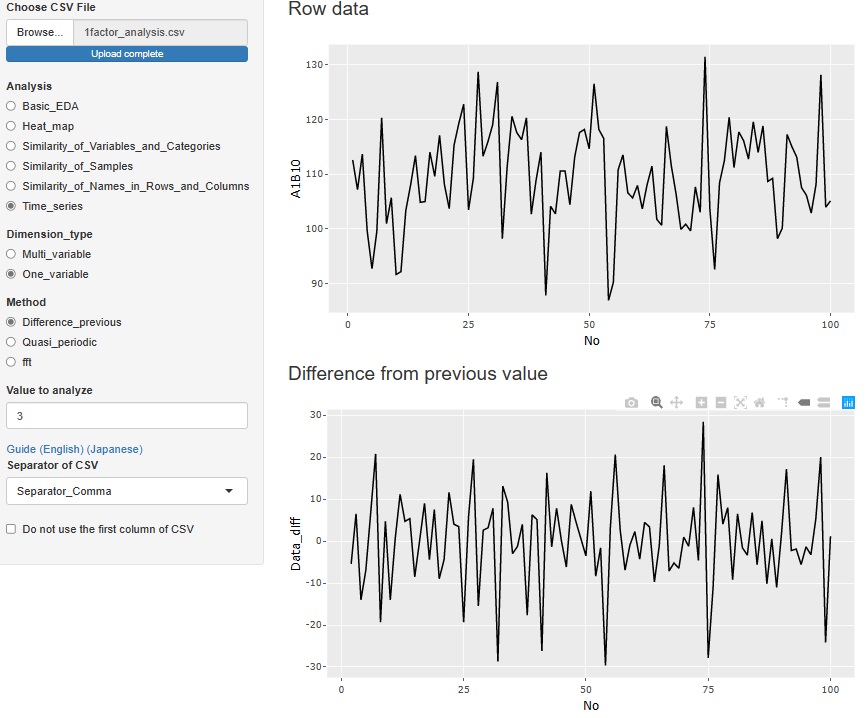
「One_variable(一変数)」の中の「Difference_previous(前との差)」は、直前のデータとの差(差分)の分析です。
一番上のグラフは、元のデータで、その下が差分をグラフにしたものです。
差分に傾向がなく、ランダムな場合は、
ランダムウォークモデル
と考えられますので、予測する時は、直前の値が一番確からしい予測値になります。
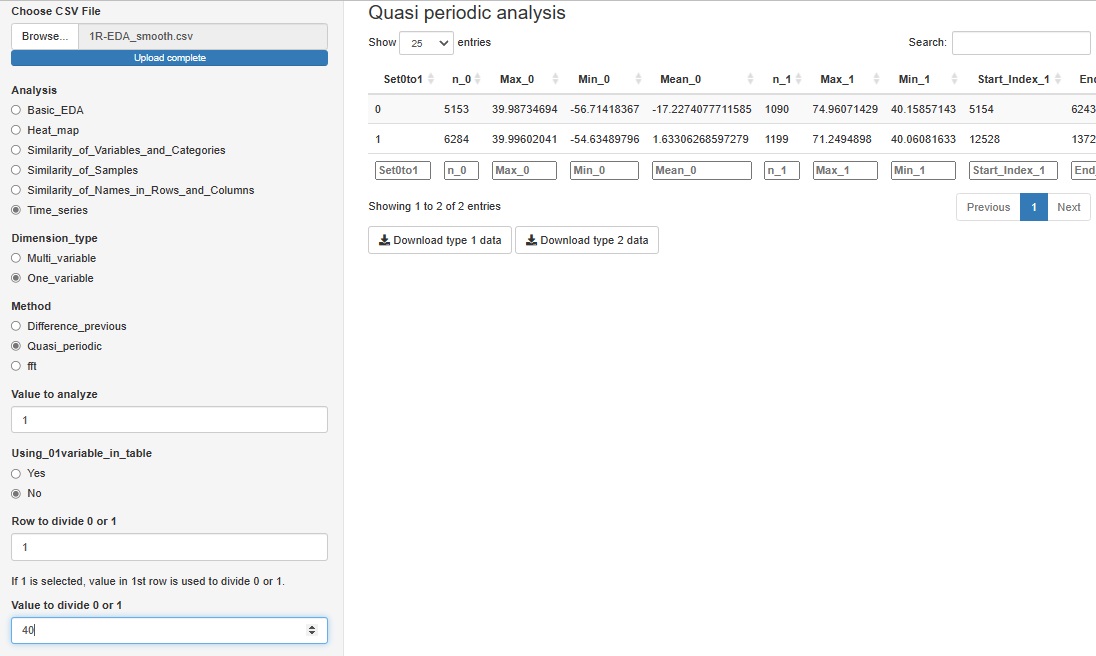
「One_variable(一変数)」の中の「Quasi_periodic(準周期)」は、工場のセンサーデータのように、
繰り返しはあるものの、周期の長さが一定ではないデータの分析をするためのツールです。
この機能は、グラフの出力はなく、
1.5次データの解析
や、
2次データ(特徴量)の解析
をするためのデータがダウンロードできるようになっています。
必要に応じて、このデータをさらに分析に使うことを想定しています。
準周期性が、1と0の数字で表されている変数があれば、それを使うことができます。
こういった変数がない場合、特定の変数について、「1列目が、40より大きければ1、40以下なら0」というようにして、こうした変数を作ることもできます。
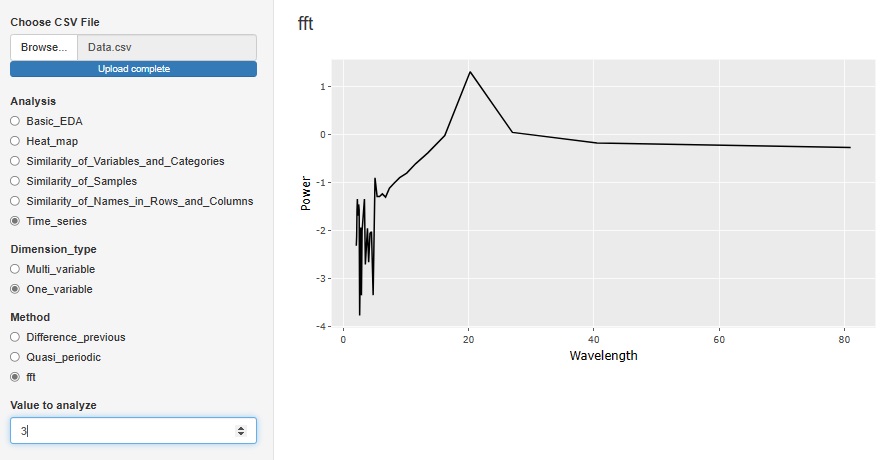
「One_variable(一変数)」の中の「fft(高速フーリエ変換)」は、
スペクトル解析
のツールです。正確な周期性がある場合の分析方法になります。
横軸は、Wavelength(波長)にしてあります。
下図の場合は、波長が20のところにピークがありますので、20行おきに周期性のあるデータであることがわかります。
「Decision_Tree(決定木)」に、「C5.0_based_RandomForest(C5.0を使ったランダムフォレスト)」を追加しました。
「C5.0」では、木は1つできますが、これは全変数、全サンプルを使って作られます。
C5.0_based_RandomForestでは、変数やサンプルの1部について、複数の組合せを選ぶことで、複数の木を作ります。 これによってデータの多様性や、似たような結果になる変数がわかるようになります。
1部のデータの選び方は、ランダムサンプリングです。 行数や列数の平方根の数を選ぶようにしてあります。 例えば、10000行のデータなら、100行が選ばれます。
「Random sampling of samples (columns)」にチェックを入れて、 「Random sampling of variables (rows)」のチェックを外すと、サンプルは1部を使って、変数は全部使う形で、複数の木を作ります。 これは「バギング」という言われている手法になります。
逆に「Random sampling of samples (columns)」のチェックを外して、 「Random sampling of variables (rows)」にチェックを入れると、変数は1部を使って、サンプルは全部使う形で、複数の木を作ります。 サンプル数が少ない場合や、因果関係の分析では、このやり方の方が知りたいことに到達しやすくなります。
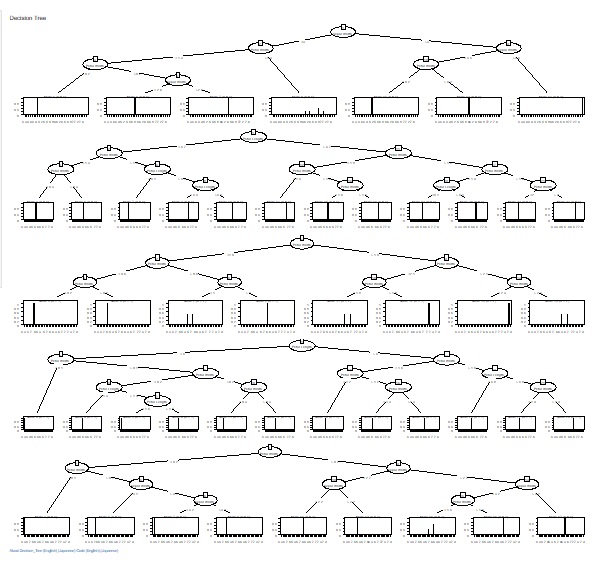
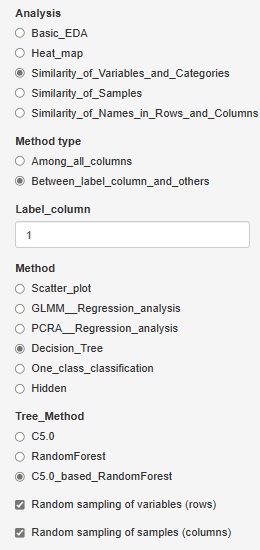
決定木を作る時の木の細かさは、デフォルトにお任せにしていたのですが、巨大な木(枝分かれが細かい木)になることがあります。 因果関係の分析では、3番目くらいまでの枝分かれがどうなるのかが重要で、巨大な木は不要なことが多いです。 また、巨大な木をOKにすると、計算時間が非常に長いことがあります。 さらに、巨大な木は、過学習とも言えることがあり、ロバストではないので使いにくいです。
そこで、枝分かれ先の最小の大きさを設定できるようにしました。
「Use minimum size of splits」にチェックを入れると、設定できるようになります。
チェックを外すと、デフォルトにお任せになります。
例えば、「Ratio of the number of minimum size」を「0.1」にすると、最小になる枝分かれは、全体の0.1になります。
1000行のデータでしたら、100よりも小さくはならなくなります。
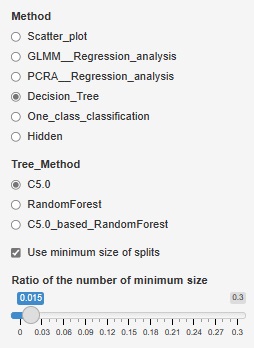
下の2つの図は、同じデータに対して、設定値を変えた場合の例です。
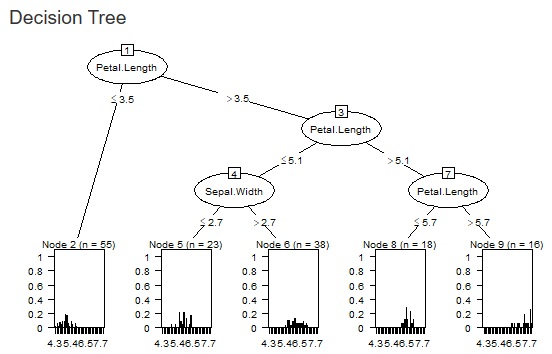
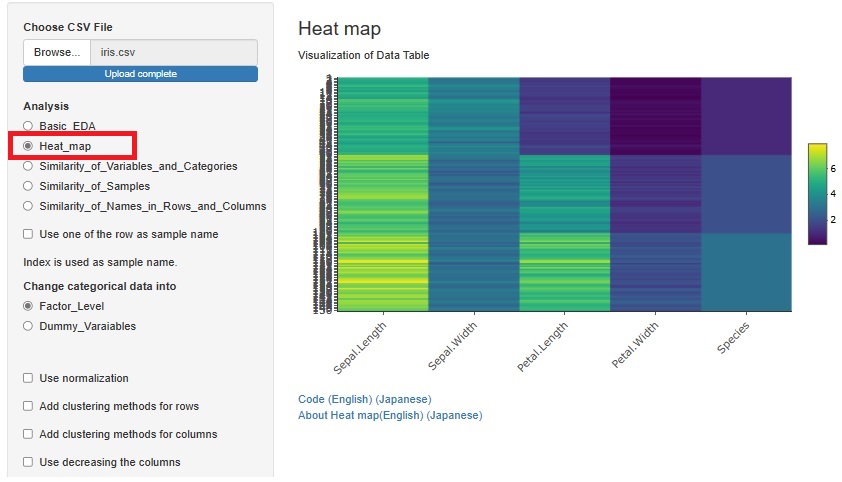
今までは、「Similarity_of_Variables_and_Categories(変数とカテゴリの類似度))」と、 「Similarity_of_Names_in_Rows_and_Columns(行と列の名前の類似性)」のそれぞれの中に、 ヒートマップを使って、データの表全体を可視化する方法を入れていました。 それぞれで少し機能を変えていました。
データの表全体を可視化する方法は、「Similarity_of_Samples(サンプルの類似度)」でも役立つのですが、入っていませんでした。
データの表全体を可視化する方法は、EDAの基本になるものですし、3種類のSimilarityの全部を分析できる方法としても他の方法とは違いますので、
「Heat_map(ヒートマップ)」は、3種類のSimilarityの分析から独立させてひとまとめにしました。
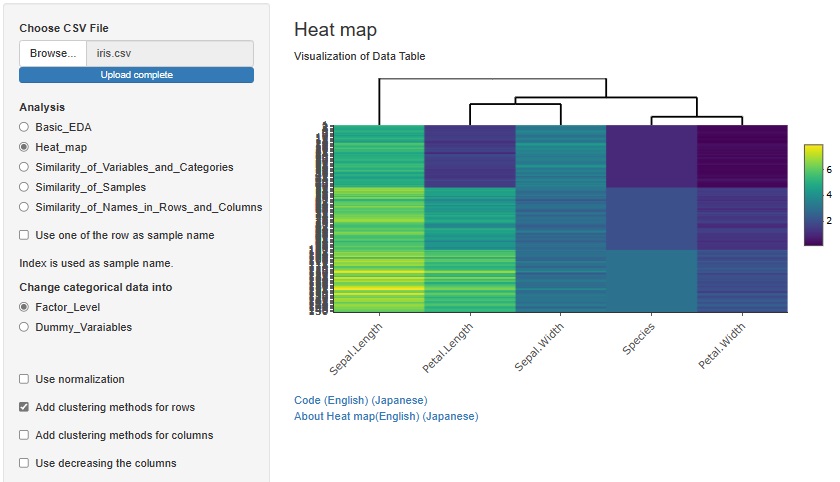
「Add clustering methods for rows」にチェックを入れると、似た変数が近くになるように並び変えられます。
「Add clustering methods for columns」にチェックを入れることで、似たサンプルを近くにすることもできます。
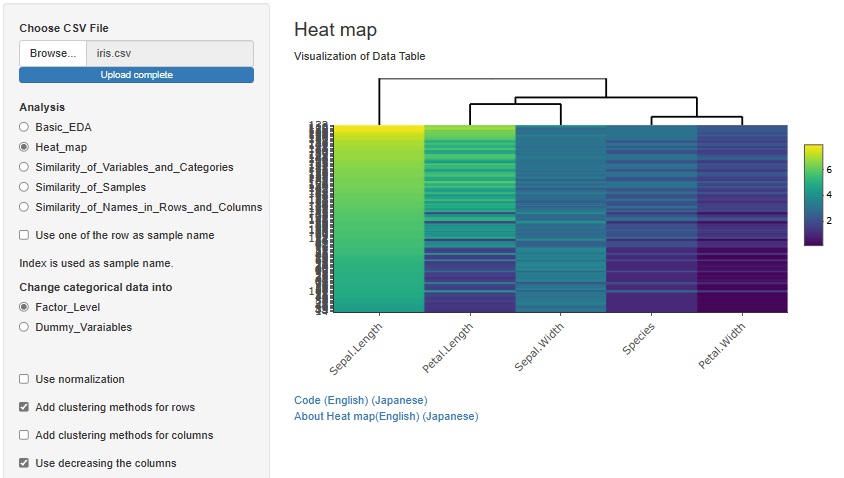
似たサンプルを近くにする方法は、もうひとつあります。
「Use decreasing the columns(行の降順を使う)」にチェックを入れると、任意の変数について降順で並べられます。
「Heat_map(ヒートマップ)」、「Similarity_of_Samples(サンプルの類似性)」、「Similarity_of_Names_in_Rows_and_Columns(行と列の名前の類似性)」の3つの分析の機能には、今まで、「データには、サンプル名の列がなければならない」、「サンプル名の列は1列目でなければならない」、という前提がありました。
今回、この2つの前提を不要にしました。
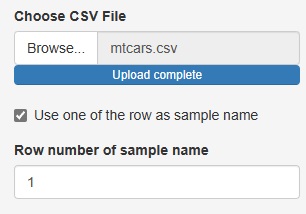
「Use one of the row as sample name」のチェックを外すと、サンプル名の列がない場合に、行番号をサンプル名の代わりにして、分析することができます。
「Row number of sample name(サンプル名の列番号)」に入れた数字の列がサンプル名として扱われます。
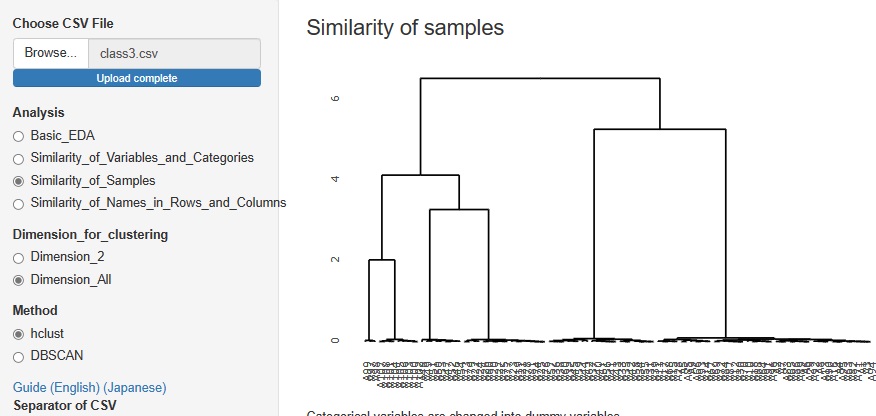
階層的な方法によるクラスター分析は、サンプルの種類が少ない時は良いのですが、ある程度多くなると、グラフに字が重なるようになり、 解読不能になります。
そのため、R-EDA1には入れていなかったのですが、インタラクティブなタイプのグラフにするのなら、解読不能ということもなくなりますので、 追加しました。
「Similarity_of_Samples(サンプルの類似性)」
→「Dimension_All"(全次元)」
と進んだ中にある「hclust」になります。
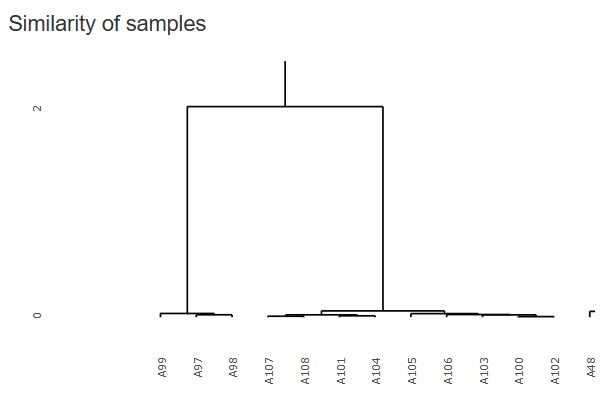
下図がインタラクティブの機能を使って、一部を拡大したものです。
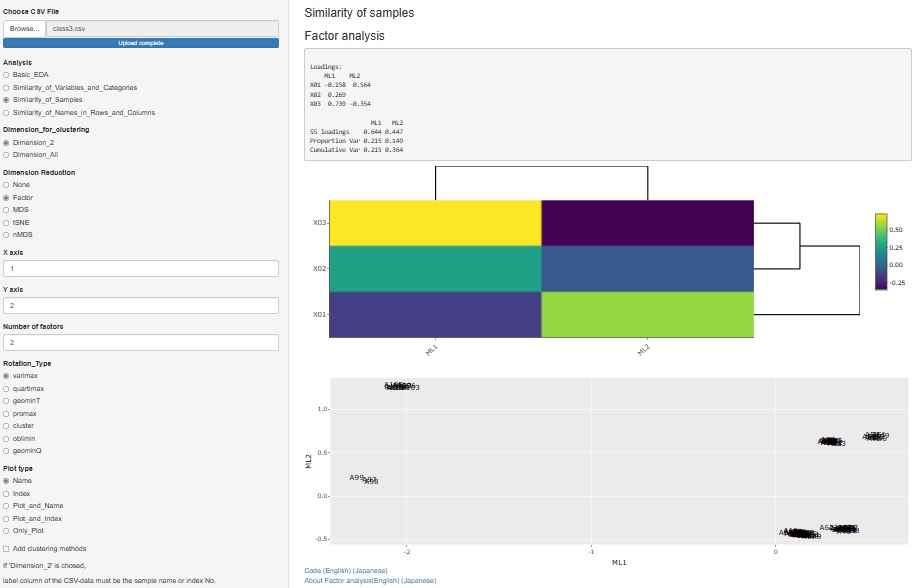
2021/09/25に因子分析のリリースをしましたが、変数の関係を分析するための機能として作っていました。 そのため、「Similarity_of_Variables_and_Categories(変数やカテゴリの類似性)」の中に組み込まれていました。
因子分析は、サンプルの類似性を因子との関係も含めて調べたい時にも使いますので、そのための機能も作りました。
「Similarity_of_Samples(サンプルの類似性)」
→「Dimension_2"(2次元)」
と進んだ中にある次元削減の種類に、「Factor(因子)」を追加しました。
2次元散布図の軸が、因子になります。
ほぼすべてのグラフが、インタラクティブなタイプに変わりました。 見た目は同じでも、見たい場所だけ拡大表示したり、マウスで個々のプロットの情報を確認できたりします。 ネットワークグラフの場合は、グラフをつまんでグリグリ動かせます。
散布図やヒストグラム:ggplotlyでplotly化
ヒートマップ:heatmaplyに変更
ネットワークグラフ:無向グラフはnetwork3D、有向グラフはvisnetwork
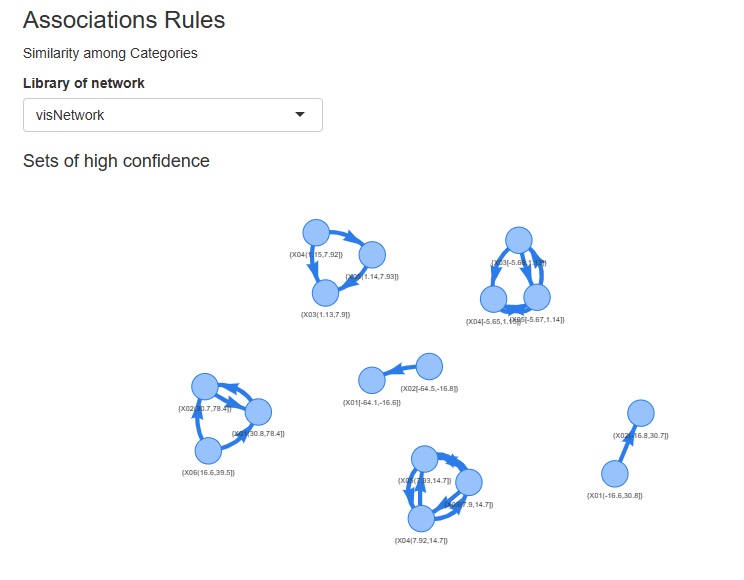
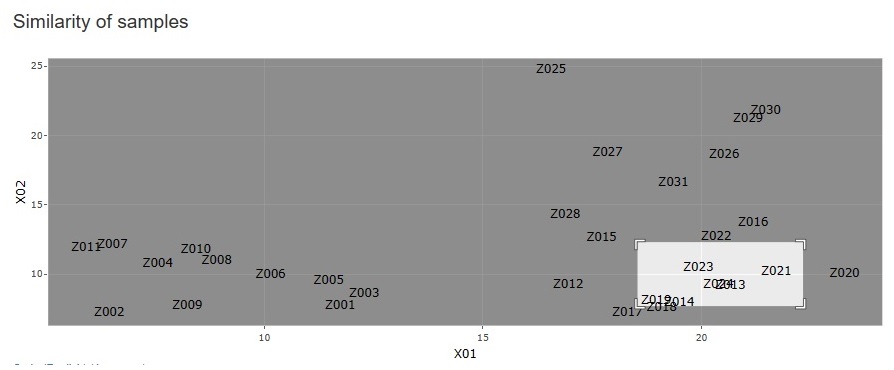
「Similarity_of_Samples(サンプルの類似性)」
→「Dimension_2"(2次元)」
と進んだ中にある次元削減の種類に、「None(なし)」を追加しました。
任意の2つの変数について、サンプル名の散布図を作れます。
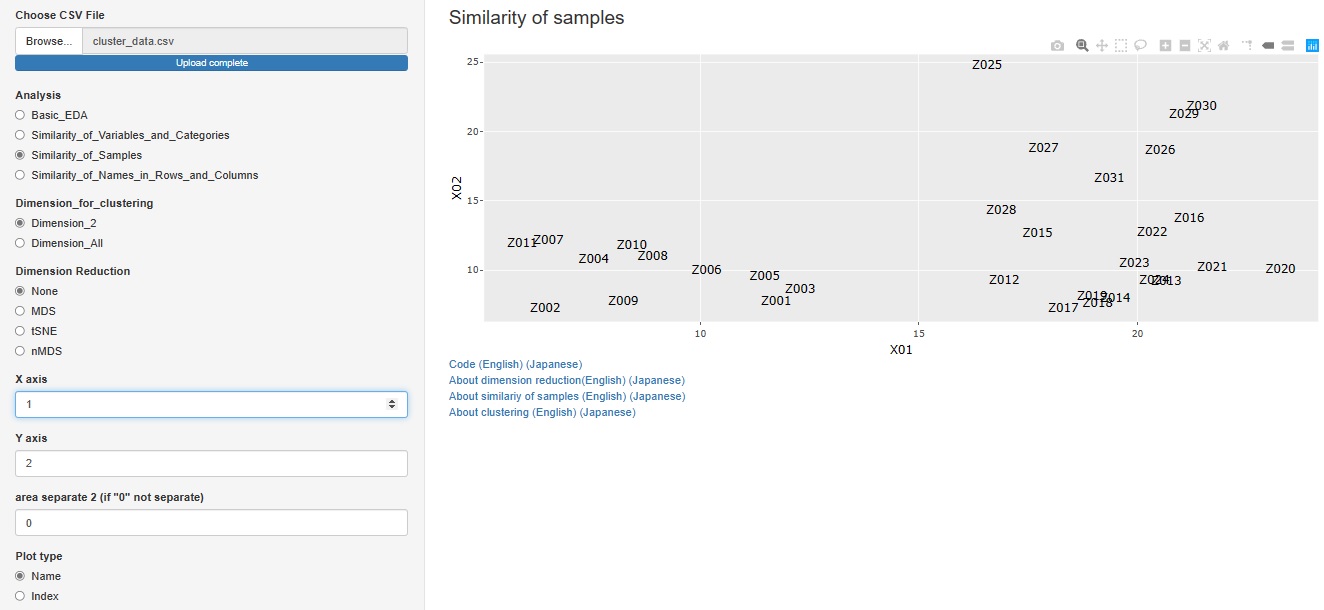
「Similarity_of_Samples(サンプルの類似性)」
→「Among_all_columns(すべての列同士)」
→「Stratifeid_graph(層別グラフ)
と進んだ中にあるグラフの種類に、「3D-scatter(3次元散布図)」を追加しました。
3次元の軸以外で、層別できるのは、色だけです
2次元散布図のようにグラフの分割はできません。
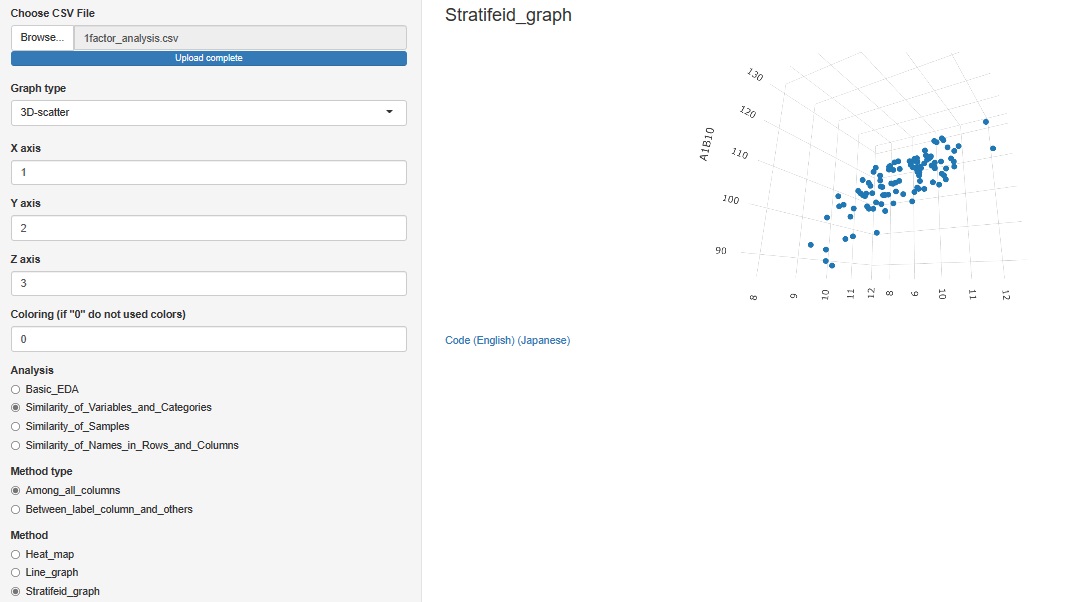
「Similarity_of_Variables_and_Categories(変数やカテゴリの類似性)」
→「Dimension_2(2次元)」
と進んだ中にある次元削減の種類に、「line_graph(折れ線グラフ)」を追加しました。
ラベルの変数の変化の中に、他の変数のカテゴリがどのように入っているのかがわかります。
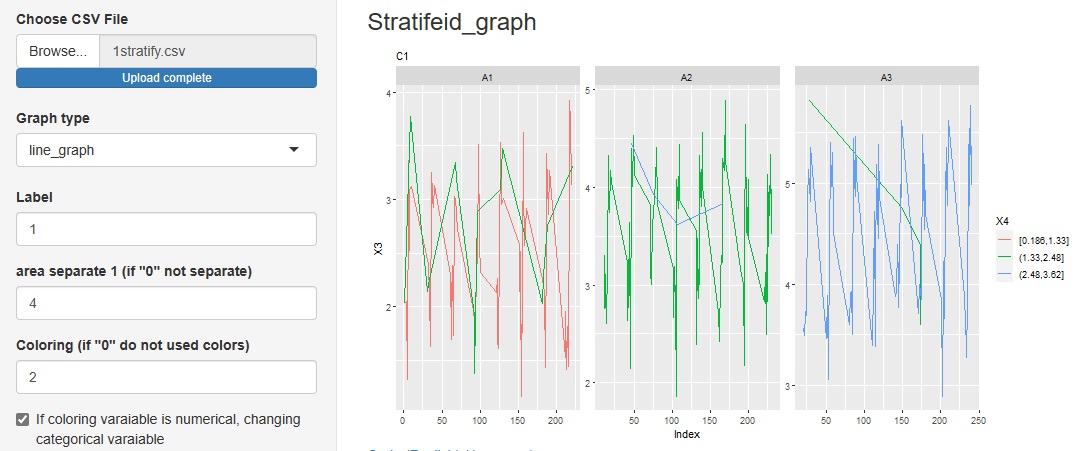

「Similarity_of_Variables_and_Categories(変数やカテゴリの類似性)」
→「Among_all_columns(すべての列同士)」
と進んだ中にあるMethod(方法)に、「Factor_Analysis(因子分析)」を追加しました。
データとして見えている変数の背後に共通因子を仮定して、それがどのようにデータに関わっているのかを調べることができます。
回転は、7種類から選べます。
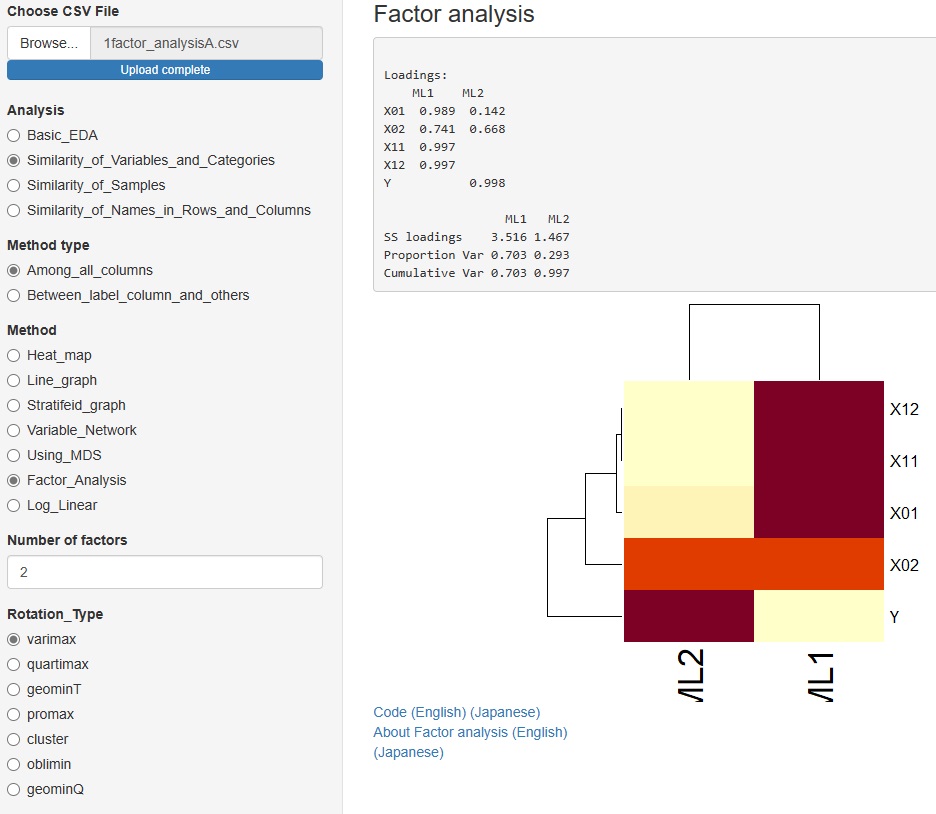
「Similarity_of_Variables_and_Categories(変数やカテゴリの類似性)」
→「Between_label_column_and_others(ラベルのと他の変数の関係)」
→「Stratifeid_graph()
と進んだ中にある「histgram(ヒストグラム)」と「scatter(散布図)」のそれぞれで予測区間を出すようにしました。
ただし、いずれもグラフを層別した時には、計算されません。
ヒストグラムは、区間が数字で表示されます。
散布図は、グラフに赤い線で表示されます。
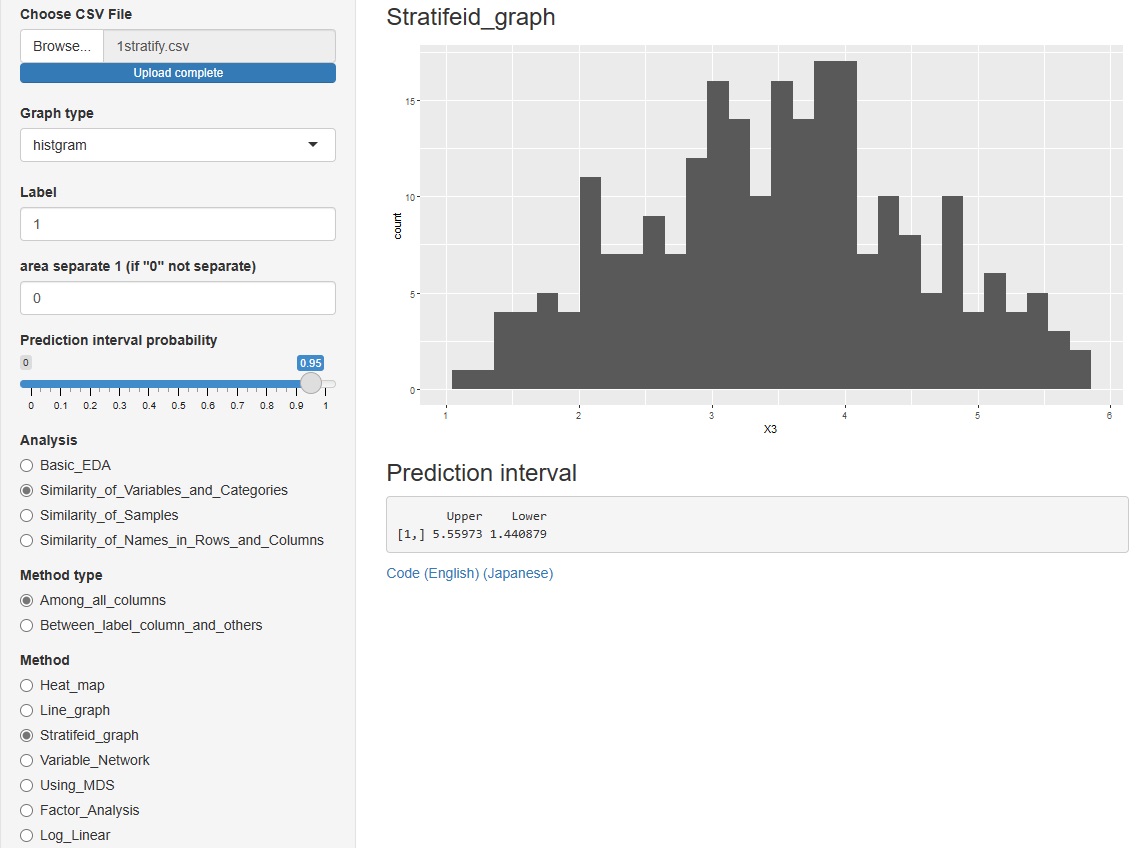
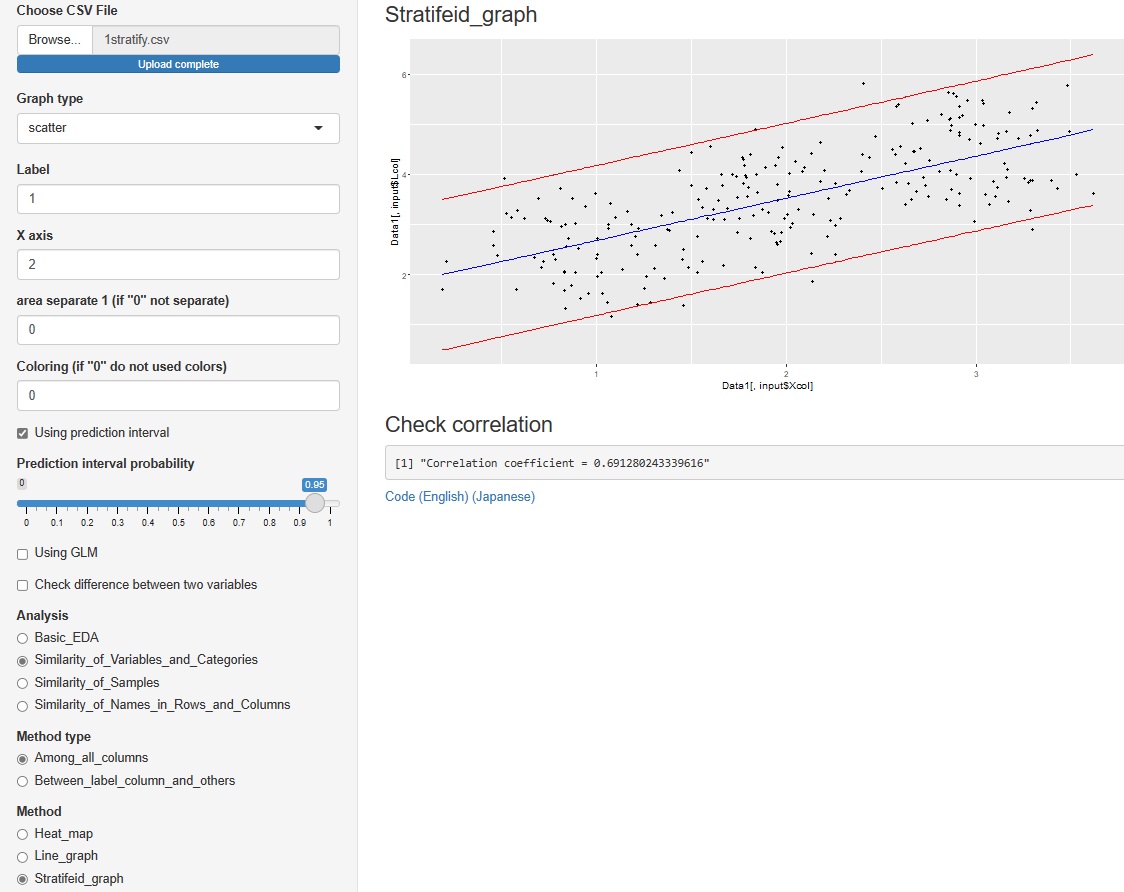
「Similarity_of_Variables_and_Categories(変数やカテゴリの類似性)」
→「Between_label_column_and_others(ラベルの変数と、他の変数の関係)」
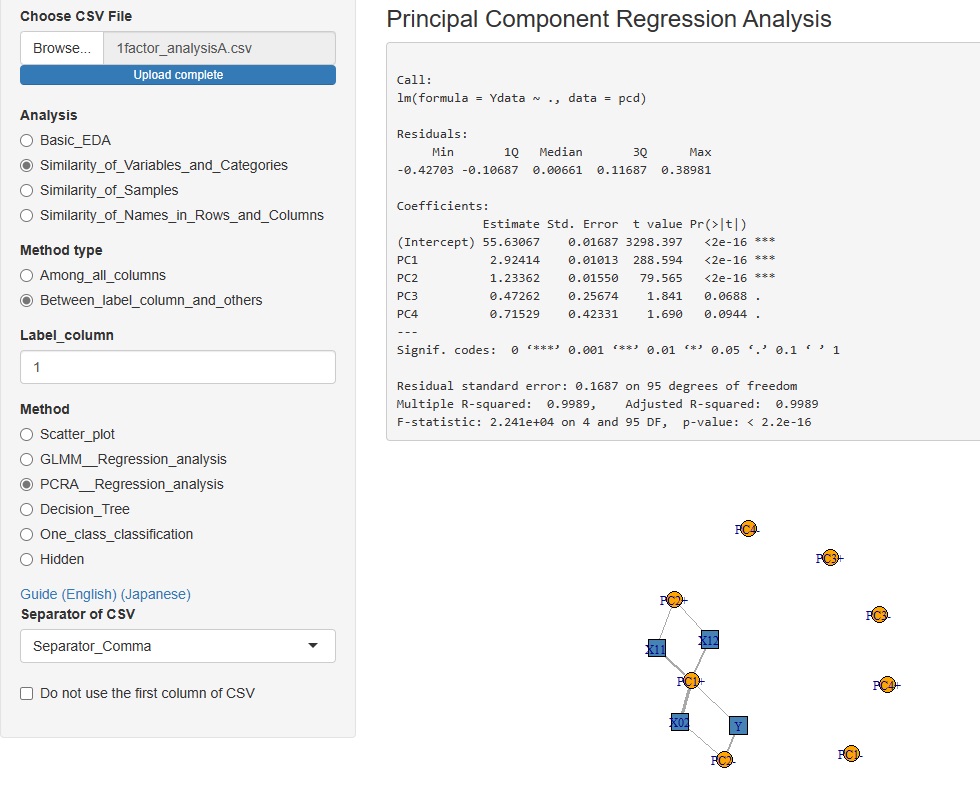
と進んだ中にあるMethod(方法)に、「PCRA__Regression_analysis(主成分回帰分析)」を追加しました。
説明変数と主成分の相関関係は、ネットワークグラフで確認できるようにしています。