トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
高次元を２次元に圧縮して可視化する方法は、ただの圧縮ではなく、「２次元に圧縮」という点が特徴です。
変数の類似度の分析 の場合は、調べたいものが変数の類似度なので、例えば、４次元に圧縮されれば、「このデータは４種類の変数を特徴にしている」ということがわかることで、次のアクションにつながります。
サンプルの類似度の分析 の場合、４次元データから、サンプルの類似度を考察しようとすると、変数同士の組合せから総合的に考えることになります。 自分は理解できたとしても、自分以外の人と理解の共有が難しいです。 そのため、 サンプルの類似度の分析 では、２次元まで圧縮することが重要になります。
２次元にすることによって、データの様子を見ることが簡単になり、データの特徴をつかみ易くなります。
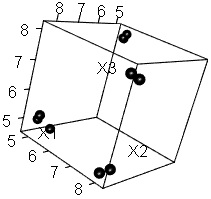
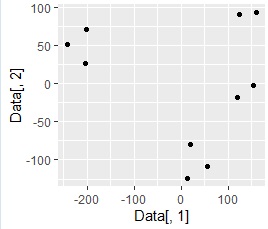
下の例は、３次元データを２次元に変換した例です。
４つのグループにサンプルが分かれていることが、
２次元散布図
で簡単にわかるようになっています。
なお、変換前のデータはもっと高次元でもできます。
-->
たくさんの列（説明変数）があるデータを ２次元散布図 を使って調べる時には、 一般的には、２列ずつの組み合わせを順に散布図にします。 高次元を２次元に圧縮して可視化する方法でも散布図を作るのですが、この散布図には、２列ではなく、すべての列の情報が入っています。
「高次元データを２次元データにする」という説明では、ピンと来ないかもしれませんが、 本来であれば２列しか表現できないはずの散布図に、たくさんの列の情報を描いてしまうのが、すごいです。
ブレーンストーミングの後に、 出てきた意見を似ているものでグループに分けてみたり、 何かのコレクションを、似ているもので近くに置いてみたりする事がありますが、 この２次元マップは、その発想に近いです。 つまり、近い場所にあるかどうかは意味があるのですが、マップ上のどこにあるのかには、あまり意味がありません。
高次元を２次元に圧縮する方法は、距離を使う方法と、変数の意味を使う方法に、大きく分かれます。
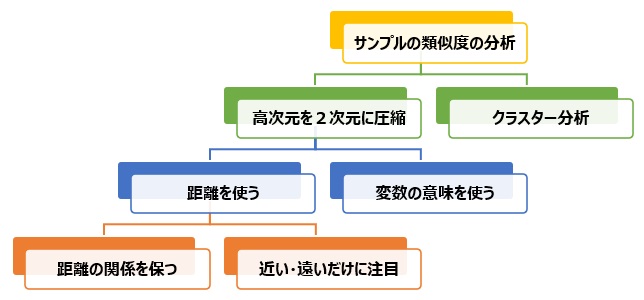
場所が座標データの形であれば、距離を計算することができます。 それと似た形で、多次元データについて、サンプル間の距離を計算することができます。 これを活用して、多次元を２次元に圧縮します。
距離を使う方法は、 距離の関係を保って２次元に圧縮する方法 と、 近い・遠いだけに注目して２次元に圧縮する方法 に分かれます。
距離の関係を保って２次元に圧縮する方法 は、多次元の中での距離を、２次元の中での距離と考えて、その距離が計算されるような２次元座標を求めます。
近い・遠いだけに注目して２次元に圧縮する方法 は、距離の関係を保つことをさらに極端にして、「近いか遠いかだけを調べる」という方針にします。
こうすると、座標の計算がなくなり、矛盾が起きなくなります。 また、シンプルで、わかりやすい方法になります。
「近ければつなぐ・遠ければつなげない」という考え方で、ネットワーク構造を作ります。 これを２次元平面に表現することができて、ネットワークグラフになります。 「次元圧縮」とは違いますが、最終的には、多次元が２次元になります。
データの中に、「目的変数と説明変数」、「原因系と結果系」という区別が最初からある場合、この情報を元にします。 ゴールにする２次元は、「目的変数と説明変数」や「原因系と結果系」が、それぞれ１次元ずつに圧縮されることを目指します。
変数の意味を使って２次元に圧縮する方法 は、このようなアプローチをしています。
次元圧縮の方法としては、 主成分分析 が有名です。
結果的に２次元に圧縮されることもあります、主成分分析は、２次元に圧縮することを目標にしたアルゴリズムになっていないです。 ３次元よりも多い時もあります。
ただ、主成分分析は、比較的軽い計算で、高次元を低次元に圧縮する能力があります。 これを活用して、２次元に圧縮する前に、前処理として主成分分析を実行することがあります。
このページは、高次元を２次元に圧縮して可視化する方法としてまとめたものですが、 このページの手法は、「次元削減」や「多様体学習」の手法として紹介される方が一般的です。
次元削減の手法として使う時は、必ずしも２次元まで圧縮する必要はなく、 中間層 として使って、モデルの計算負荷を減らしたり、モデルをわかりやすくするために使います。 この目的で使う時は、 「多少無理があってでも、高次元データを２次元データに圧縮する方法」よりも、 主成分分析 の方が、使いやすいです。
「高次元を２次元に圧縮して可視化する方法」としては、 主成分分析 よりも、「多少無理があってでも、高次元データを２次元データに圧縮する方法」の方が良いので、優劣が逆転しています。
高次元を２次元に圧縮する方法は、パラメータを変更すれば、３次元や１次元にも圧縮できるようになっていることもあります。 特に指定しなくても使える方法は、デフォルトが「２」になっています。
３次元に圧縮する場合は、次元圧縮としての使い道はあるかもしれませんが、「マップで見る」という使い方には不向きです。
１次元に圧縮する場合は、「グループに順番を付ける」という使い道ができそうですが、 なんの指標もなく、高次元を１次元に圧縮したデータは、１次元の値に意味がないので、順番を付ける使い方ができません。 それもあり、１次元への圧縮も積極的に使う用途がないように思っています。
なお、上記は、１次元の量的データに圧縮する時の話です。 高次元の量的データを、１次元の質的データに変換する方法としては、 クラスター分析 があります。 １次元にするのなら、質的データの方が使い道があります。
順路
次は
高次元を２次元に圧縮する方法の比較
