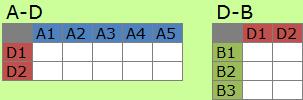
関係性の解析では、行列分解によって、A-B型の行列を2つの行列の積に分ける事があります。
Dの要素数がAやBの要素数よりもはるかに少なくなって、
複雑な行列の特徴が簡単に表現できる事があります。
Aの特徴をDで表現でき、Bの特徴もDで表現できるようになります。
このため、Dの要素は、特徴やパターンと呼ばれます。
パターンの抽出は、 クラスター分析 の一種ですが、このパターンがAとBの関係性の要約になっている点が、 一般的に知られているクラスター分析とは異なります。
テキストマイニング の場合は、パターンは「トピック」や「潜在意味」と呼ばれます。 この分析は、「トピックモデル」と呼ばれています。
それぞれの単語が、どのような分野でよく使われるかが解析でき、また、それぞれのテキストがどのような分野のものなのかが解析できるようになります。 （応用として、単語が分かれば、そのテキストの分野が当てられる（予測できる）ようになります。）
行列の分解は、「特異値分解」と呼ばれる代数学の方法が、比較的古くから採用されて来たそうです。
この方法は、 テキストマイニング では、「潜在意味解析」と呼ばれています。 LSIやLSA（Latent Semantic Indexing、Analysis）とも呼ばれます。
特異値分解は、Rなどのソフトでは「SVD」という名前です。 主成分分析 や 自己組織化マップ の仲間として分類されています。
LSIでは、特異値が負になってしまう場合の解釈に困る事や、 「データを確率的な現象のものとして扱いたい」、という考えから、 PLSI（Probabilistic Latent Semantic Indexing）やLDA（Latent Dirichlet Allocation）と呼ばれる方法が発達したそうです。
潜在変数の確率モデルという点では 因子分析 に近く、 確率のネットワーク構造を使うという点では、 ベイジアンネットワーク に近い方法です。
「非負行列分解（NMF）」として分解する方法もあります。 非負行列分解は、行列の値が負の値にならない事と、パターンの数がAやBよりも少ない事を条件として、 行列を分解します。
この分解によるパターンは独立にはならないですのですが、これはデータによっては、望ましい性質です。
例えば、テキストデータの分類の場合、大多数のテキストに含まれる単語を第一主成分のようにして扱ってしまうと、 良い分類にはなりません。 このような単語は、どの分類にも振り分けられるようにして、頻度の少ない単語で分類した方が、良い分類になりやすいです。 独立にならない性質は、テキストデータのこのような性質に対して、うまく機能してくれます。
Rによる実施例は、 Rによる行列の分解 のページにあります。
「Rで学ぶクラスタ解析」 新納浩幸 著 オーム社 2007
混合分布 ： 確率モデルによるクラスタリング
スペクトラルクラスタリング ： グラフの分割（カット）によるクラスタリング
第8章が「次元縮約（高次元データから低次元データへ）」となっていて、
その手法として、特異値分解、LSI、PLSI、NMFが紹介されています。
次元縮約は、高次元行列のクラスタリングの前処理として行われる場合と、これのみでクラスタリングとして使われる場合がある。
LSIは、特異値分解そのもの。
NMFは縮約後の軸が直交しない。この特徴はテキストの分類の用途には適している。
ファジィクラスタリングは、ソフトクラスタリングの別名。
混合分布モデルやNMFは、ソフトクラスタリングの一種。
狭義のファジィクラスタリングとして、Fuzzy c-meansがファジィクラスタリングと呼ばれている事がある。
「関連性データの解析法 多次元尺度構成法とクラスター分析法」 齋藤尭幸・宿久洋幸 著 共立出版 2006
二者関係を表すデータ解析として、多次元尺度構成法とクラスター分析を解説しています。
筆者は、クラスター分析はA-B型のデータ用のものと思っていましたが、
A-A型
からスタートするものもあるそうです。
「関係データ学習」 石黒勝彦・林浩平 著 講談社 2016
関係データとは、行列の値が２つのものの関係性を表しているデータの事です。
関係データの扱い方について、2016年時点までの最新の情報をまとめているそうです。
分析の目的は知識抽出と予測。
知識抽出としてクラスタリング。
予測は欠損値の推定を使う。
2章が固有値問題による行列のクラスタリング。
主成分分析
に近い方法。
3章がクラスターを仮定し確率モデルとしてクラスタリング。
因子分析
に近い方法。
確率モデルにすると、データのばらつきに対応できたり、固有値問題で解けない場合に対応できる利点があるが、
モデルの作り方で分析してわかる事が変わるので、考える事が多いのが難点。
事前分布を仮定し、事後分布を求める、という
ベイズ統計
になる。
4章が行列分解で、i行j列の行列を、i行k列とk行j列の行列の積にする方法。
kとして出て来るものが、元の行列のパターンを表す。
自然言語処理の分野では、このパターンはトピックとして解釈される。
行列の分解をするための最適化計算のアルゴリズムが、丁寧にまとまっています。
5章6章で行列分解がテンソルに拡張される。
行列分解では2つの事柄の関係までしか分析できないが、テンソルが扱えると、3つ以上でも扱える。3つ目を時系列データにすると、時系列解析にもなる。
行列の分解には、A-Bの行列をi-k、k-k、k-jの行列に分解する方法があります。
テンソル分解のタッカー分解は、k-kのような部分を作る所が似ています。
この本は、前半が行列を固有値なので、そのままの形で要約するアプローチで、後半は行列やテンソルに分解して要約するアプローチです。
著者が違うせいかもしれませんが、これらのアプローチの関係がよくわかりませんでした。
RでNMFをする手順は、下記を参考にさせていただきました。
http://rstudio-pubs-static.s3.amazonaws.com/22351_00c2376922f548ddb0870904dd42a098.html
「データマイニング入門 ：Rで学ぶ最新データ解析」 豊田秀樹 編著 東京図書 2008
ひとつの章が
潜在意味解析
になっています。
約20ページで、潜在意味解析の概要を学び、Rで実際に実施してみるところまで、できるようになっています。
「トピックモデルによる統計的潜在意味解析」 奥村学 監修 佐藤一誠 著 コロナ社 2015
p.24までで、トピックモデルがどういうものであるのかを、丁寧に解説しています。
行列の特異値分解には、文章と単語の行列を、文章とトピックの行列、トピック同士の行列、単語とトピックの行列、
という３つの行列の積にする性質があるそうです。
そして、このモデルの問題の解決として、統計的なモデルが構築されたそうです。
この後は、モデルの学習方法、潜在意味空間（トピックを変数とする空間）を扱う教師付き学習、
文書の時系列モデリングの章が続きます。
「トピックモデル」 岩田具治 著 講談社 2015
確率モデルのバリエーションを、数学の言葉で説明している本です。
順路
次は
A-B型の中間層分析
