ベイズ統計では、経験や信念等、計算に取り入れにくいものを取り入れられます。 既知の事象の知識を使って、観測できない確率を計算してしまうという使い方もできます。
計算のよりどころは、ベイズの定理です。
ベイズ統計学は、ここから理論が広がっています。
筆者なりにまとめると、下図のようになっています。
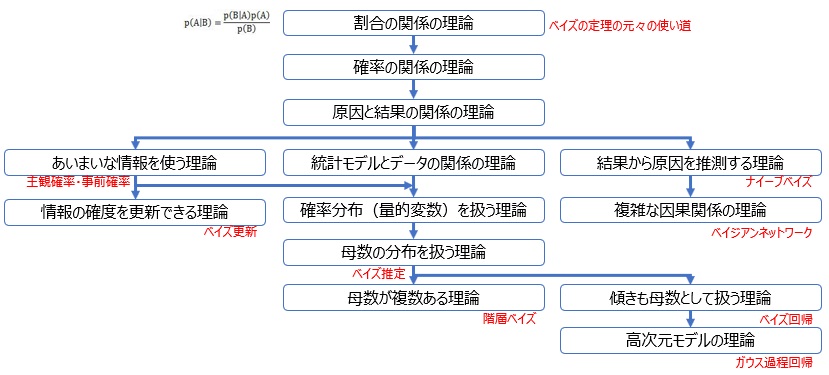
ベイズの定理は、
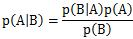
と書かれます。
例えば、
P（A）＝ みかんが好きな人の割合、
P（B）＝ りんごが好きな人の割合、
P（B|A）＝ みかんが好きな人の中で、りんごが好きな人の割合、
P（A|B）＝ りんごが好きな人の中で、みかんが好きな人の割合、
と考える事ができます。
「P（A）、P（B）、P（B|A）のデータがあれば、P（A|B）のデータがなくても、P（A|B）は計算で求める事ができる。」、 というのが、ベイズの定理の意味です。
ベイズの定理はベイズ統計の重要なものですが、 ベイズの定理自体は、とてもシンプルなものです。
上記では「割合」という言葉を、あえて使ってみました。 「確率の式」と考えてしまうと、実感がわきにくいと思いますが、 ベイズの定理を理解するには、「確率」という言葉は使わなくても大丈夫です。
ベイズ統計は、原因の解析や意思決定の理論に使われますが、 「りんごが好きな人の中で、みかんが好きな人の割合」という感じでベイズの定理を理解する段階では、こうした使い方はできません。
P（A）、P（B）、P（B|A）、P（A|B）をいろいろなものに応用する事で、原因の解析や、意思決定の理論になって来ます。
ベイズの定理の「割合」とした部分を「確率」と考えると、応用範囲が広がります。 何かを当てる精度を扱う理論として使えるようになります。
ベイズの定理で、「P（A）を原因を表すもの、P（B）を結果を表すもの」、と考えると、ベイズの定理の使い道がぐんと広がります。
例えば、「P（A）は故障している確率、P（B）はセンサーが反応する確率」と考えます。 故障とセンサーの反応が必ず一致するのなら、ベイズ統計を使う事もないのですが、 故障してもセンサーが反応しないとか、逆に、故障していないのにセンサーが反応すると言った事が現実にはあります。
「センサーが反応した時に、実際に故障している確率はどの程度か？」、という計算をするのに、ベイズの定理が役に立ちます。
実際の計算では、
P（A）＝センサーが反応するかどうかに関係なく、とにかく故障している確率
P（B）＝故障していて反応する確率と、故障していないのに反応する確率の合計
P（B|A）＝故障した時に、センサーが反応する確率
の３つのデータが必要になります。
これらを使って、P（A|B）を計算します。
ちなみに、
故障していないのに、センサーが反応する確率 ＝ 1 - P（B|A）
ですので、「センサーが反応した時に、実際は故障していない確率」も同じようにして求める事ができます。
この理論は、ナイーブベイズや、ベイズフィルターと呼ばれています。
ベイズの定理で扱うものを「故障とセンサー」のような関係のものにすると、 「故障」そのものを確認できなくても、故障しているかどうかを推測する事ができます。 つまり、ベイズの定理は、直接知る事ができない事を、知るための理論になります。
別の見方をすれば、「センサーの反応」という結果から、「故障発生」という原因を推測するための理論になっていますので、 ベイズの定理は、 逆問題 を解くための理論とも言えます。
原因と結果を表すものが、ひとつずつなら、上記の計算で良いのですが、 世の中では、原因の現象と結果の現象がいくつもあって、複雑な構造をしている事がよくあります。
計算が複雑になるものの、基本的な考え方はひとつずつの場合と同じです。 原因と結果がいくつも考えられる計算は、 ベイジアンネットワーク と呼ばれ、フリーソフトもあります。
上記の故障の例では、センサーが反応するかどうかに関係なく、初めは故障している確率がP（A）と考えています。 「センサーが反応」という事実がわかった時に、 故障していると考えられる確率が、P（A|B）として計算され、認識が変わります。
この事から、
P（A）は事前確率、
P（A|B）は事後確率と呼ばれます。
「P（A）は事前確率」と考えるようにすると、ベイズの定理の使い道がさらに広がります。
例えば、センサーが１回反応するよりも、２回反応する方が、故障している確率は高いと考えられますが、 この確率を計算する時は、１回目に反応した時に計算した事後確率を、２回目に反応した時の事後確率を計算する時の事前確率として使います。
こうした計算をベイズ更新と言います。
ベイズ更新によって、ベイズ統計は得られたデータをどんどん採用する事によって、 最初に設定した確率から、 より確からしい確率を求める理論になって行きます。 持っている情報が増えるたびに、考え方を修正していくというものですので、人間の 認知と学習 の仕組みとも、とても似ています。
なお、 機械学習 には、 逐次学習 と呼ばれるものがあります。 逐次学習も、新しいデータがえられるためにパラメタを更新するところは、ベイズ更新と同じですが、逐次学習と呼ばれているものは、 必ずしもベイズ統計ではないです。 例えば、逐次学習 のページにあるように、一般的な平均値の計算も、逐次学習の形に変形して計算することができます。
ベイズ更新によって、事前確率はどんどんデータによって修正されますので、 事前確率は、「最初に仮に使う数字」や、「計算の初期値」程度になります。
このため、事前確率には、「たぶんこうだろう」という感じの主観的な確率（主観確率）を使うことができます。
主観確率を使うと、「自分が最初に思っていたものを、データで修正する」という使い方になります。
ベイズ統計は主観確率を有効に使う理論です。 ところが、「観測していないことを前提にすることは、科学として認められない。」という立場の人にとっては、 主観確率は認められない概念です。 ベイズの定理は、200年前の理論ですが、統計学の専門家の間では長い間論争があり、 支持しない立場をとる方もいらっしゃるそうです。
ところで、立場どうこうの前に、現実の世界では、主観確率は役に立っています。 信頼性工学の「FMEA」や「FTA」 のように、主観確率を積極的に使っている手法もあります。 未知（未観測）の現象に挑戦していくのに、主観（経験）が役に立っています。
母数というのは、正規分布だと、母平均と母分散の２つのパラメタのことです。
上記のベイズの定理に対して、
P（t） ⇒ その母数が得られる確率
P（D|t） ⇒ その母数によって、そのデータが得られる確率
P（D） ⇒ そのデータが得られる確率
、とすると、
P（t|D） ⇒ そのデータが得られた時に、その母数になる確率
となります。（「t」は「θ」と書く文献が多いです。）
こうすると、ベイズの定理が母数とデータの関係を表していることになります。
回帰分析の傾きのようなパラメタも母数の一種です。
上記のベイズの定理に対して、
P（t|D）とP（t） ⇒ 「確率分布」
P（D|t） ⇒ 「尤度」
P（D） ⇒ 「定数」
、として、確率分布（確率の確率）を考えるようになると、ベイズの定理の応用がさらに広がります。
ベイズの定理が、統計の理論らしくなって来ます。
「みかん・りんご」や、「反応あり・なし」のような質的変数ではなく、量的変数を扱う理論になって来ます。
ガウス過程回帰分析 は、これのかなり高度なものです。
上記で、P（t）を「その母数が得られる確率」として、さらにそれが「確率分布」としました。 これは、「母数が確率分布を持っている」ということを前提とした話になっています。
ベイズ統計学では、母数は固定された数値ではなく、分布しているものと想定しています。
例えば、一般的な回帰分析では、傾きは固定値として考えて、この値を求めようとします。 ベイズ統計の回帰分析では、傾きの事前分布と事後分布を見ようとする分析になります。
階層ベイズ では、さらに発展して、「母数は複数ある」というモデルを考えます。 それぞれの母数が分布しているものであることに加え、そうしたものが複数重ね合わさっているモデルになっています。
ちなみに、「母数が複数ある」ということは、ベイズ統計学ならではの話ではなく、非ベイズ統計学では、混合モデルと呼ばれて、母平均が複数あって複数の正規分布の山があるモデルがあります。
「「超」入門ベイズ統計 結果から原因を推理する」 石村貞夫 著 講談社 2016
架空の事件の犯人探しを例にして、ベイズ統計を説明しています。
最終的には、ベイズの定理で、犯人の確率を計算します。
その前に必要な、個々の事象の発生確率は、クロス表、
ロジスティック回帰分析
、
ニューラルネットワーク
、といったもので計算していました。
「見えないものをさぐる―それがベイズ 〜ツールによる実践ベイズ統計」 藤田一弥 著 オーム社 2015
ベイズの定理の実際の使われ方まで、平易な説明でたどり着けるようになっていました。
病気を確率で診断するのにベイズの定理を使う
→ ベイズ決定（意思決定の理論。
それぞれの確率にその場合の損失をかけて、足し合わせる事で、損失を試算して、どちらの行動の方が損なのかを選ぶ）
ベイジアンネットワークをフリーソフトのWekaで
→ 確率分布
→ 大きな集団の情報を事前分布として、小さな集団の情報の確からしさを上げる
→ カルマンフィルタ（動的に状態が変わる時の理論）
「ベイズな予測 ヒット率高める主観的確率論の話」 宮谷隆 著 リッツテレコム 2009
数式をあまり使わずに、言葉による説明で、ベイズ統計の特徴を説明しています。
ナイーブベイズ
の応用の話が多いです。
ベイズ統計を、「チャンスを生かす」、「予測と洞察」に使えるものとしています。
主観的な確率を使えること、個別の確率を使えること、確率の変化を扱えることの話と、
様々な産業での利用の可能性の話があります。
「理工基礎 確率とその応用」 逆瀬川浩孝 著 サイエンス社 2004
確率で使う道具を順に解説していて、
条件付き確率のところでベイズの定理が出てきます。
「史上最強図解 これならわかる！ベイズ統計学」 涌井良幸・涌井貞美 著 ナツメ社 2012
ベイズ統計の考え方を、漫画や図解をたくさん使いながら丁寧に説明しています。
同じ著者の下記の本と比べると、Excelでの計算例は引かれています。
「道具としてのベイズ統計」 涌井良幸 著 日本実業出版社 2009
ベイズの定理に、確率密度関数や尤度という考え方を入れるプロセスが丁寧に説明されています。
つまり、統計学や微積分に不慣れな人に親切です。
多くの話題を扱っている訳ではないですが、
MCMC法
や、
階層ベイズ
等の重要な項目について、見通しの良い解説をしています。
「Excelでスッキリわかるベイズ統計入門」 涌井良幸・涌井貞美 著 日本実業出版社 2010
「道具としてのベイズ統計」よりも入門的な内容に限定されていますが、
さらに整った形にまとめられています。
例題に取り組むことを繰り返して、段階的にベイズ統計の考え方に入っていくようになっています。
Excelで計算する流れも具体的に書かれています。
「身につくベイズ統計学」 涌井良幸・涌井貞美 著 技術評論社 2016
事典と入門書の間のような本です。
ナイーブベイズ、ベイジアンネットワーク、回帰分析、階層ベイズ法、等もあります。
一般的な回帰分析では、回帰係数が外れ値の影響を受けやすいですが、
ベイズ統計による回帰分析では、事前分布が緩衝材の役割をするので、そのような事が起きにくいそうです。
「ビジネスマンがはじめて学ぶ ベイズ統計学 ExcelからRへステップアップ」 朝野煕彦 編著 朝倉書店 2017
実務への利用を念頭に置いて、例を
マーケティング
の題材にしながら、基本的なところから丁寧に説明されています。
ベイズ統計と従来の統計学で違いが出るのは、階層ベイズモデル。
階層ベイズ
は、個人では少量データだけれども、たくさんの人のデータがあるような時に、
「個性」を考慮することができるモデル。
「ビジネスマンが一歩先をめざす ベイズ統計学 ExcelからRStanへステップアップ」 朝野煕彦 編著 朝倉書店 2018
上記の本の続編です。
MCMCの応用として、仮説の検証と、予測分布。
階層ベイズ
の応用として、
状態空間モデル
。
ベイズ統計学の信用区間を使うことによって、パラメタの分布や予測分布を出すことができることが、
ベイズ統計学が従来の統計学の
検定
よりも便利な点として挙げられています。
（この説明には、従来の統計学にある
信頼区間と予測区間
の話がありませんので、信用区間が信頼区間や予測区間よりも役に立つというわけでもないように思いました。
ただし、これらの区間の計算に、「事前・事後」という概念が入れられるかどうかは、ベイズ統計学の便利な点と思います。）
状態空間モデルを、実際に使う時はリアルタイムなデータの更新と予測になりますので、
ベイズ更新のアイディアと共通点があります。
そのため、両者を合わせた理論は、とても便利なようです。
「しくみがわかるベイズ統計と機械学習」 手塚太郎 著 朝倉書店 2019
ベイズ統計の解説の後に、EMアルゴリズム、グラフィカルモデル、変分ベイズ、マルコフ連鎖モンテカルロ法、変分オートエンコーダを、
ベイズ統計と関連付けながら解説しています。
「はじめての統計データ分析 ベイズ的<ポストp値時代>の統計学」 豊田秀樹 著 朝倉書店 2016
ベイズ統計学は、母数の分布を想定するのに対して、一般的な統計学は母数を固定して考えることを違いとしています。
また、ベイズ統計学は、データを得た上で事後分布を計算する形で結論を出すもので、コンピュータの発達でMCMC法が使えるようになったことで、
実用的になったとしています。
これらの背景を前提として、分布、母数、平均値の差の分析、といった統計学の入門的な話題を、ベイズ統計学の視点で解説しています。
いったんベイズ統計学の立場で考えるようになると、一般的な統計学の方が不自然な方法論になるそうです。
「統計学入門 1 生成量による実感に即したデータ分析」 豊田秀樹 著 朝倉書店 2022
同著者の「はじめての統計データ分析」を、改めて書き直したような内容になっています。
この本もベイズ統計を基本とした本です。
「効果がある」、「違いがある」という事は統計学では言うことができず、そのように言える量をドメイン知識から決めて、それとの関係を調べる方法を紹介しています。
「統計学入門 2 尤度によるデータ生成過程の表現」 豊田秀樹 著 朝倉書店 2022
回帰分析
、
ポアソン回帰分析
、
ロジスティック回帰分析
、
数量化理論
、
項目反応理論
等を、ベイズ統計の書き方で説明しています。
「ベイズ統計の理論と方法」 渡辺澄夫 著 コロナ社 2012
スッキリ書かれているようには思うのですが、数学ならではの書き方に慣れていない方（筆者がそうですが）には難解な本です。
相転移
も出て来るので、面白い本だと思うのですが、、、
「ベイズ統計学入門」 渡部洋 著 福村出版 1999
分布・平均・回帰等について、すべてベイズ推測という視点で書いてあります。
「ベイズ推定入門 モデル選択からベイズ的最適化まで」 大関真之 著 オーム社 2018
タイトルがベイズ推定ですがベイズ統計らしい話はあまりありません。
この本の中心は
スパースモデリング
や
カーネル法
で、ベイズ統計はこの本で紹介されている正則化やの背後にある話として位置づけられています。
「ベイズ統計学とその応用」 鈴木雪夫・国友直人 編 東京大学出版会 1989
意思決定の話や、主観確率や事前確率についての論考があります。
難しい本です。
「ベイズ統計と統計物理」 伊庭幸人 著 岩波書店 2003
統計物理学（イジングモデル等）を勉強した方限定ですが、
この本はベイズ統計学の入門書になると思います。
遺伝学・氷・磁性体・画像修復が、同じ本の中で書かれている点でも面白い本です。
統計物理学のマルコフ連鎖モンテカルロ法（MCMC法）が、
ベイズ統計に使われているのは、アナロジーがあるからだそうです。
著者の修士論文は、氷がテーマとのことでした。
くしくも筆者も氷を修士論文で扱ったので、たのしく読ませていただきました。
筆者は「セラミックか。氷か。」、で迷っていた時に、
「万物の根源は水」という指導教官の一言で氷を選びました。
「氷は身近な物質なので、今さら調べることなんてないのでは？」、
と思う方もいらっしゃると思いますが、
そうでもないです。
「マンガでわかる量子力学」 川端潔 監修 石川憲二 著 柊ゆたか 作画 オーム社 2019
量子の世界が、量子力学としてまとめられるまでの歴史的な話が、楽しくまとめられています。
電子を、波動と見るか、粒子と見るかといった解釈に確率論が導入された部分は、統計学を勉強した人にとっては興味深く読める部分ではないかと思います。
分布と観測の関係はすんなり読めると思いますが、
ハイゼンベルクの不確定性原理のような考え方や、
多重に存在している点は違和感があるかと思います。
量子力学が形成される途中では、量子は確率的な存在と考えて観測者は明確に考えて来たけれども、1950年代になって、「多世界解釈」というものができ、
観測者も確率的な存在と考えるようになったそうです。
この部分を読んだ時に、
ベイズ統計では、統計モデルのパラメータを確率的に考えることを筆者は思い出しました。
次は
生成モデルと識別モデル
