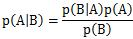
Bayesian statistics use known probability to calculate unknown probability. Bayes' theorem is core point.
Bayes' theorem is written as
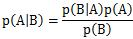
P(A) is "prior probability". P(A|B) is "posterior probability".
We can calculate chain probability with this theorem over and over.
When the probability has network connection, the calculation system is called Bayesian Network .
Bayesian Statistics consider "P(A|B)" and "P(A)" as probability distribution.
"P(B|A)" as likelihood.
"P(B)" as a constant number.
Likelihood is calculated with measured data.
Prior distribution is given subjectively.
We consider "constant", because we can normalize with sum of probability.
By this consideration, we can get posterior distribution by revising subject with measured data.
Bayesian statistics use subjective probability effectively.
This theory was built about 200 years ago. But some people who thinks "It's not science that use not observed data", does not understand subjective probability. This is not a dispute about science but philosophy.
By the way, in a practical case, subjective probability is important. For example, FMEA and FTA use subjective probability positively. "Subject" in other words "experience" is useful to try strange fields.
Diversity is important in environment. And diversity is also important in quality of high-mix low-volume production".
Considering equality is not preferable in diversity analysis. I think, Bayesian statistics is preferable in diversity analysis. Especially, "Hierarchical Bayes" may be the best.
NEXT 
Generative Model and Discriminative Model
