 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
一括学習はバッチ学習、逐次学習はオンライン学習と呼ばれることもあります。
一括学習は、 機械学習 の一般的な解説の中で、特に「一括」とは付けずに、学習の手順として紹介されることが多いです。
「データを集め、学習してモデルを作る。」という手順のことで、その後に予測や判定と言ったことを始めます。
逐次学習は、その名の通りで、新しいデータを得るたびに、モデルを更新して、常に最新モデルを使って予測や判定をする方法です。
逐次学習の特徴は、以下になります。
世の中で、「ビッグデータ」が注目され始めた時に、その処理方法が課題になりました。 一括学習では、一時的にコンピュータのメモリを大量に使う必要があるため、ビッグデータの処理は無理でした。
いくつかの解決策のひとつが逐次学習でした。
逐次学習では、1回前の学習結果、つまりモデルのパラメタを、新しいデータを使って修正します。 この計算の時に、過去のデータのすべてをもう一度参照する必要がなく、過去のデータで作ったモデルのパラメタだけを参照するため、 メモリをあまり使わずに済むアルゴリズムになっています。
一括学習では、学習が1回終われば、基本的にそのモデルを使い続けます。 「データが増えて来たので、モデルを作り直して、精度を上げたい」、という場合は、改めて過去からのデータを準備して、学習の作業をやり直す必要がありました。
前述のように、一括学習では、メモリを多く使うため、学習のやり直しができなかったり、できたとしても非常に時間がかかったりします。 一方、逐次学習では、常に最新状態のモデルを準備することができます。
良く知られている平均値や分散は、逐次学習で計算することができます。
逐次学習は、非定常データの理解にも役立ちます。 例えば、 見せかけの回帰 のページで使っています。
n番目までの平均値を求めるのに、n番目のデータと、n-1番目までの平均値があれば良いことが、この式からわかります。
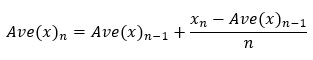
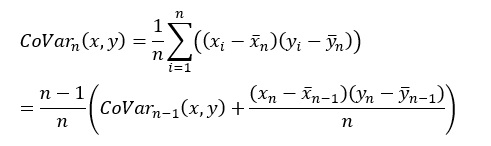
上の式で、yをxに変えると、分散の式になります。 それの平方根は、標準偏差の式になります。
例えば、「平均値の真の値は、5.3」となっているデータに対して、平均値の逐次学習をすると、下図のようになります。
青い点がデータで、赤が平均値です。
グラフの左から右の方向で、サンプル数が増えています。
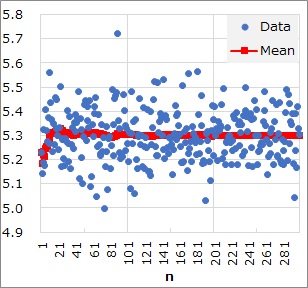
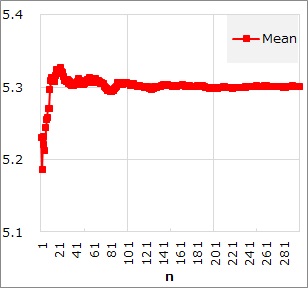
このグラフからは、「サンプル数が少ないほど、平均値の確からしさが低い。」という見方もできます。 この確からしさを、定量的に表す方法としては、 標準誤差 があります。
この例の場合では、n=200あたりから、平均値はほとんど変わらなくなっています。 このように、逐次学習では、値が収束していきます。 真の値があるのなら、それに近付きます。
上記の逐次学習のアルゴリズムは、真の値が一定なことを想定しています。 真の値が変化していく現象の場合、上記のような逐次学習のアルゴリズムは合いません。
そのような場合、平均値については、 移動平均 、 ARモデル 、 指数平滑法 があります。
標準偏差については、 ボラティリティ推定モデル があります。
ベイズ統計 に「ベイズ更新」と呼ばれる方法があります。
ベイズ更新も逐次学習の一種として使えます。 ベイズ更新の場合は、一括学習の式を変形して逐次学習にするのではなく、ベイズ統計の式自体がもともと逐次学習に使える形になっています。
「オンライン機械学習」 海野裕也・岡野原大輔・得居誠也・徳永拓之 著 講談社 2015
オンライン学習だけでなく、人工知能や機械学習の歴史や勉強の仕方から、解説が始まっています。
ただし、扱っている機械学習は、
ニューラルネットワーク
、
サポートベクターマシン
、
ロジスティック回帰分析
になっていて、2クラス分類問題を扱う話が中心です。
多クラス分類が少しあります。
回帰分析
のようにYが量的データの話はありません。
全体的には、オンライン学習の技術の中心は、確率的勾配降下法による最適化ですが、
この話だけではなく、計算を安定させたり高速にするための関数の話もかなりされています。
機械学習の多くのモデルは、バッチ学習の方法として、もともと作られているので、
オンライン学習にするには、目的変数を考えてから、これを確率的勾配降下法にしてアルゴリズムを求めます。
ニューラルネットワーク
は、もともとがオンライン学習の方法として作られていますが、他の方法と同様に目的変数を考えてから、
オンライン学習のアルゴリズムを導出するという流れでも、説明されています。
ディープラーニング(深層学習)
の場合に解を求めるための工夫の話もあります。
オンライン学習の強み:計算が速い。実装が簡単。大量のデータの保持が不要。
オンライン学習の弱み:ノイズの影響を受けやすい。
オンライン学習の基礎になるのが、確率的勾配降下法。
勾配降下法は、目的変数の勾配を使って、最適値を見つける方法。
確率的勾配降下法は、データをひとつずつ使って、その都度パラメータを更新する。
ロジスティック回帰では、解を安定させるために、
正則化
項を加える。
「製造現場の突発的な変動の影響を受けたデータにおける異常検知の改善」 杉原哲朗 著 OMRON TECHNICS 2023
https://www.omron.com/jp/ja/technology/omrontechnics/2023/OMT_Vol56_002JP.pdf
平均値や分散の逐次学習を使って、
MT法を応用しています。
順路


 次は
AIの説明可能性・解釈可能性
次は
AIの説明可能性・解釈可能性

