マージンを最大化する計算式は、全部のデータを使うようにできていますが、
実際に計算を進めると、最終的な直線の式に必要なのは、直線に特に近いデータだけになるそうです。
このデータはサポートベクターと呼ばれます。
サポートベクターマシン（SVM ： Support Vector Machine）は、一本の直線（正確には超平面）を引いて、 その直線のどちら側に行くのかで、判別しようとします。 この点は、 判別分析 と同じです。
ちなみに、「ベクター」というのは、日本語では「ベクトル」と呼ばれることが多いです。 「サポートベクトルマシン」と訳している本もあります。
一本の直線の見つけ方として、サポートベクターマシンではマージンの最大化という方法を使います。 マージンの最大化によって、 過学習（オーバーフィッティング） や、局所最適（良さそうなモデルがいくつかあった時に、一番初めに見つかったモデルで良いと考えてしまう）を避け、 新たなデータに対してもできるだけ余裕のある（汎用性の高い）モデルを作ろうとします。
マージンというのは、判別の直線に特に近いデータと、直線との距離です。 この距離が長ければ長いほど、汎用性が高いと考えます。
マージンを最大化する計算式は、全部のデータを使うようにできていますが、
実際に計算を進めると、最終的な直線の式に必要なのは、直線に特に近いデータだけになるそうです。
このデータはサポートベクターと呼ばれます。
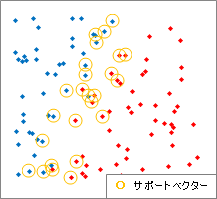
RapidMinerで計算すると、どれがサポートベクターなのかも出力されています。 右の図は、その出力を使って、元のデータでサポートベクターになったものに、印を付けてみたものです。
最終的には、サポートベクターの計算だけで済んでしまうという性質は、
「計算量を小さくする」、
「元のデータの全体的な分布に、計算が影響されにくい。（ロバスト）」、
「古典的な
多変量解析
と違って、
正規分布
を仮定しない。」、
という事でもあります。
「計算量を小さくする」については、 カーネル法 を使って、もっと計算量が大きくなる時にも、活きて来ます。
「元のデータの全体的な分布に、計算が影響されにくい。」や、「古典的な多変量解析と違って、正規分布を仮定しない。」については、 古典的な解析では想定外のデータを扱う時に活きて来ます。
サポートベクターマシンにも、弱点はあります。
マージンの最大化をするには、領域を分ける線が、はっきりしている必要があります。 ソフトマージンの理論があるので、一本の線で分けた時に、少しは分類が間違うデータがあっても大丈夫なのですが、 全体を見渡した時には、領域を分ける線が見えている必要があります。
領域がぼやけている場合、特に、2つの群の判別で、片方の群の発生確率が1/2を超える領域がない場合は、 サポートベクターマシンは結果を出せません。
世の中には、一本の直線で判別しようとする事が難しい場合があり、これが一本の直線で判別する方法の弱点です。 カーネル法 は、このような場合でも、一本の直線で判別しようとする方法を使えるようにしてくれます。
カーネル法は、サポートベクターマシンの研究の中で考え出されたそうですが、 現在では、 ガウス過程回帰分析 や ロジスティック回帰分析 等の、サポートベクターマシン以外の用途でも使われています。
「サポートベクターマシン」 小野田崇 著 オーム社 2007
事例で、
センサーデータの解析があります。
カーネル関数は、扱っている問題に適したものを選ぶ事が大事としています。
「パターン認識のためのサポートベクトルマシン入門」 阿部重夫 著 森北出版 2011
サポートベクターマシンの様々なバリエーションが紹介されています。
ファジィ理論
や、
マハラノビスの距離
とからめたものもあります。
「サポートベクターマシン入門」 Nello Cristianini・John Shawe-Taylor 著 共立出版 2005
サポートベクターマシンで使われる数学の部分を、やさしくコンパクトにまとめた本として作られているようです。
「フリーソフトではじめる機械学習入門」 荒木雅弘 著 森北出版 2014
機械学習
全般の本ですが、
ニューラルネットワーク
と、サポートベクターマシンの違いなどがコンパクトにまとまっています。
「データマイニング入門 ：Rで学ぶ最新データ解析」 豊田秀樹 編著 東京図書 2008
サポートベクターマシンがひとつの章になっています。
サポートベクターマシンは、「本質的には３層のニューラルネットワーク」としています。
「Rによるデータサイエンス」 金明哲 著 森北出版 2007
このページの説明の仕方とは逆で、
カーネル法を先に説明してから、カーネル法を使う代表的な方法としてサポートベクターマシンを紹介しています。
サポートベクターマシン以外でカーネル法を使う方法として、
カーネル主成分分析も紹介しています。
順路
次は
カーネル法
