という式ですが、これはデータが直線状に並んでいる時にしか、うまく当てはまりません。
ガウス過程回帰分析は、非線形の 回帰分析 の一種です。
例えば、YとXの変数がひとつずつある場合、
最初に考えるのは、
単回帰分析
の
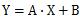
という式ですが、これはデータが直線状に並んでいる時にしか、うまく当てはまりません。
そこで、次に考えるのは、
重回帰分析
の
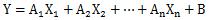
の式にある、たくさんのXのところに、Xの2乗や、対数、三角関数などの様々な関数を入れる方法です。
こうすると、直線以外の線でも表現できるようになります。
ガウス過程回帰分析も複雑な関数を仮定する点は、この考え方と同じです。 ただし、 カーネル を使うので、どのカーネルを使うのかの選択はあるのですが、関数の組合せの中身を、ひとつずつ自分で決める必要がありません。
また、ガウス過程回帰分析の特徴として、モデル式が「１本の線」にはならない点があります。 線のグループ（分布）になります。 それらの線が集まって束になっている部分は、データが集まっていて、線の確からしさが高い領域です。 反対に、線がばらけている部分は、データがなかったり、データがばらばらで、線が決めにくい領域です。 （こういうことがわかるのが、ガウス過程回帰分析の面白さのひとつですが、 回帰分析の予測区間 にもあるように、一般的な回帰分析でこうした分析がまったくできない訳ではないです。）
ベイズ統計 にある母数の分布の考え方を回帰分析に取り入れると、ベイズ統計的回帰分析になります。 事前分布から事後分布を求める理論になります。
ガウス過程回帰分析は、 カーネル を使って、複雑な形状を扱えるようにした「カーネル回帰分析」と呼べる方法に、ベイズ統計の考え方を取り入れています。
ガウス過程の「過程」というのは、時間軸に沿って確率的に値が決まってくる現象のことです。 ランダムウォークモデル などがあります。
ガウス過程は、いろいろな時刻でデータを取った時に、値が”多次元”の 正規分布 （ガウス分布）になっている確率過程です。 ちなみに、”１次元”の場合は、同じ物を繰り返し測った時の測定値が身近な例です。
ところで、ガウス過程のモデルには、時間軸が関係ありません。 元のデータからは、測定時刻の近さがわかるとしても、モデルの中ではその情報は使われません。 そのため、時間の情報がないデータについても、ガウス過程の理論は使うことができます。
ガウス過程回帰分析もそうですが、近年の「ガウス過程」の話題は、確率過程ではない現象について、ガウス過程の理論を使ったものになっています。
ガウス過程には、 ニューラルネットワーク （ ディープラーニング ）と比べて、「ほぼ同じもの」や、「数学的（解析的）に扱いやすい」という話題があります。
画像認識の分野においては、 カーネル法 を使う サポートベクターマシン が先に脚光を浴びたものの、後から登場した ディープラーニング に汎用性の高さで負けて、主流が変わったのが歴史のようです。 ところが、 カーネル法 を使う手法が再び話題になり始めたのは、興味深いです。
「ガウス過程と機械学習」 持橋大地・大羽成征 著 講談社 2019
ガウス過程回帰分析の基礎から、ニューラルネットワークとの関係などの話題まで、網羅されています。
0章：たった10ページで、ガウス過程回帰分析をわかりやすく概説。
1章：回帰分析
2章：ガウス分布
3章：ガウス過程。ガウス過程回帰分析では、あるXが与えられた時のYは、分布として求まる。
予測値としてひとつの値が知りたいのなら、この分布の期待値を求めることになる。
（リッジ回帰は係数に制約を設けることで適度な値の係数が求まることと同じような理由で、係数にガウス分布を仮定することが、
カーネル関数を使った高次元のモデルの係数が求まることになっているようです。）
4章：確率的生成モデル
5章：計算法。ガウス過程回帰分析は、計算が膨大になることがネックと考えられていたが、改善されて来ている。
6章：
空間統計学
とベイズ最適化への応用。空間統計学は、もともとガウス過程回帰分析が想定しているモデルと近いものを考えていたため、
ガウス過程回帰分析の対象として良いようです。
ベイズ最適化は、標準偏差が大きいところ（よくわからないところ）の実験条件は、実験回数を増やすような実験をするのに良いようです。
7章：ガウス過程による教師なし学習。ガウス過程潜在変数モデル（GPLVM）は、カーネル主成分分析と似ていますが、潜在変数を仮定する点が違いになるそうです。
理論的には、クラスタリングにはGPLVMの方が良いようですが、計算は難しいようです。
ガウス過程力学モデル（GPDM）は、自己相関モデルのような時系列モデルです。
時系列データを離れて発展したガウス過程の理論を、再び時系列データの世界に戻していて面白いです。
この後に、このモデルにガウス過程ではなくポアソン過程（Cox過程）を使うモデルも紹介されています。
「Gaussian Processes for Machine Learning」 Carl Edward Rasmussen and Christopher K. I. Williams 著 MIT Press 2006
もともと本として出版されたもののようですが、今は、ネットで無料で読めるようにしているようです。
英語です。
http://www.gaussianprocess.org/gpml/chapters/
回帰問題だけでなく、分類問題の章もありますし、他の手法との比較の話もあります。
「ベイズ深層学習」 須山敦志 著 講談社 2019
この本は、
ニューラルネットワーク
を解く方法として、ベイズ統計を導入する本として作られています。
・カーネルリッジ回帰をベイズ化したものが、ガウス過程。
・ニューラルネットワークをベイズ化したものが、ベイズニューラルネットワーク。
・ガウス過程とベイズニューラルネットワークを合体したものが、深層ガウス過程（教師あり）
、といった図もあります。
7章は、ガウス過程の説明の後で、深層学習との関係の説明があります。
ニューラルネットワークよりもベイズニューラルネットワーク、
サポートベクターマシン
よりもガウス過程が良い理由として、不確実さをモデルに考慮できる点を挙げています。
「確率と確率過程」 武田一哉 編著 オーム社 2010
確率論について、広く平易に書かれています。
確率過程の章の最初で、ガウス過程が出て来ます。
・ガウス過程は、正規確率過程とも言うそうです。
・n個の確率変数（データ）を持って来た時に、それが n変量の正規分布になっているのをガウス過程ということの他に、この
線形和
も正規確率密度関数にしたがう確率変数になる。
特に、この確率変数が独立で、平均μ、分散0の場合は、正規白色過程（正規ホワイトノイズ）
順路
次は
スプライン
