ニューラルネットワーク

ニューラルネットワークは、神経細胞の仕組みを真似て学習する方法です。

世の中では、ディープラーニング（深層学習）が注目の技術として脚光を浴びて来ていますが、これはニューラルネットワークの一種です。

ニューラルネットワークによる、複雑なものの表現

シグモイド関数は、Xの変化に対して、０から１の間に範囲が決まっているYを出力する関数です。右図が基本形になります。 Xが5以上で、ほぼ1になり、Xが-5以下でほぼ0になっている様子がわかります。

この性質を使うと、数量化理論を使って、１と０にしたカテゴリデータを扱ったり、確率を表現するのに便利です。

シグモイド関数のXの部分を、複数のXによる線形和にすると、いろいろなカーブを表現できる関数として使えます。

ただ、このカーブの曲がり具合には限度があり、単調減少か、単調増加しか表現できません。

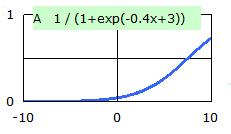
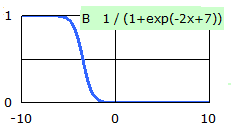
右の２つの例は、シグモイド関数によるいろいろなカーブの例です。

シグモイド関数とXの線形和で作ったカーブはひとつの関数になります。この関数の線形和を作ると、単調減少や単調増加以外の複雑な形状を表現できるようになります。

この「関数の線形和」が、ニューラルネットワークでは中間層になっています。

理論上は、中間層を重ねれば重ねるほど、複雑なものを表現できるようになります。

ニューラルネットワークでは、「Xの高次の項を入れる」、「特殊な関数を使う」、ということはせずに、線形和、シグモイド関数、中間層の３つのアイディアの組み合わせで、非線形の複雑な関数を表現できるようになっています。

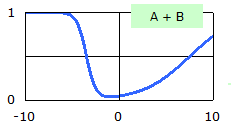
右の図は、上の２つのカーブを、単純に足し合わせてみたものです。

中間層を入れたモデルを考えることは簡単ですが、 「線形和の係数をどのようにして、計算するか？」、というのが、実際には大変な所になります。ニューラルネットワークの歴史は、この計算方法の改良の歴史と言えるようです。

計算方法は、誤差逆伝搬法が最初の突破口だったようです。誤差逆伝搬法では、試行錯誤して作った関数と本当のＹの誤差を評価して、層を逆戻りして修正をかける方法です。

自己組織化マップや、ディープラーニングはそれぞれが一冊の本になるほどですが、ニューラルネットワークの仲間と言われています。ちなみに、自己組織化マップは、人工知能の技術というより、データマイニングの技術と考えた方がしっくりします。

なお、このサイトでは、シグモイド関数やそれに近い関数で、神経細胞の仕組みを真似たモデルを「ニューラルネットワーク」と呼んでいます。

しかし、世の中の解説では、サポートベクターマシンのようなものでも、モデルの中に中間層を含む方法は、すべてニューラルネットワークのように呼ばれていることもあります。

ボルツマンマシンも、もともと神経細胞のモデルではありませんが、数学的に似た構造を持っていたり、ディープラーニングの実現に貢献したこともあって、ニューラルネットワークの一種のように紹介されています。

ニューラルネットワークのひとつのパーツは、Ｙがひとつで、Ｘが複数になっています。ＹとＸをつなぐ計算は、ロジスティック回帰分析と同じです。

ロジスティック回帰分析では、１と０の間の確率を表すために、この関数を使っています。ニューラルネットワークでは、この関数の線形和をさらに考えることで、非線形の複雑な関数を表現できるようにしています。

ニューラルネットワークは、画像認識等のパターン認識や、予測を目的とした技術としては、大変な威力が知られています。

しかし、中間層が複雑過ぎて、ブラックボックスになってしまうので、因果推論の手法には向かないです。

※　ブラックボックスの部分を、もっと人間が認識しやすい形にできれば、使い道は増えて来るかもしれません。

「データマイニング入門　：Rで学ぶ最新データ解析」豊田秀樹　編著　東京図書　2008
ニューラルネットワーク、自己組織化マップが、それぞれひとつの章になっています。
サンプルコードや、サンプルデータもあり、Ｒを使って自分で試せるようにもなっています。

「複素ニューラルネットワーク」広瀬明　著　サイエンス社　2005
複素数を使うニューラルネットワークの歴史から応用まであります。
電磁波の振幅と位相のデータから、対象物の形状の画像を作る技術になるようです。