数量化理論は、 定性的な情報を、数量で扱うための理論です。
数量化理論の計算方法は、 多変量解析 と言われている方法が基本になっています。
しかし、 多変量解析 の方法が、基本的に変数の関係を見るために使う方法であるのに対して、 数量化理論の使い道は、 決定木 や カテゴリの類似度の分析 と似ています。 そのため、このサイトでは、数量化理論を データマイニング の枠の中に入れるようにしました。
歴史的には、 アンケート・感性評価 のデータの分析方法として考案された方法から、 テキストマイニング の方法として使われるようになっています。
数量化理論の話の中には、「数量化」の作業が２段階になっていて、まったく異なる視点の数量化を２回行います。
１段階目が、質的データを多変量解析の手法で扱うための数量化です。
Ⅰ、Ⅱ、Ⅲ類では ダミー変換 をする作業が「数量化」です。 Ⅳ、Ⅴ、Ⅵ類では、感覚的な大きさをアンケートなどを使って、数字にする作業が「数量化」です。
２段階目が、各サンプルや、質的変数のカテゴリの数量化です。
Ⅰ、Ⅱ、Ⅲ類で使うダミー変換されたデータは、1と0しかない離散データになっている量的変数の集まりですが、 これを連続的な数値の量的変数に変換することもでき、これが「数量化」になります。 また、ダミー変換する前の質的変数のカテゴリや、Ⅳ、Ⅴ、Ⅵ類で使うデータの行と列のカテゴリは、質的なデータですが、 これらに対応する数値を求めることもでき、これも「数量化」になります。
もともと数量化理論は、上記の２段階目まで行う手法として開発されて来ています。 心理学の分野など、アンケートなどを使って得られたデータから、定量的な分析を進めるための方法になっています。 数量化の２段階目まで進めたデータを使います。
２段階目まで進めたデータを、 特徴量エンジニアリング をしたデータのように考えて、量的変数の方法で扱うこともできます。 質的変数のグループを、１つの連続変数に変換 がこれに当たります。
世の中でも、数量化理論は、質的変数のデータを量的変数の方法で扱うための方法として、 理解されることが一般的になって来ているようです。
目的変数と説明変数の関係を調べたり、説明変数から予測モデルを作ったりする使い道で、Ⅰ類、Ⅱ類を使います。
この使い道の場合は、数量化の２段階目の作業は必要なく、１段階目のデータだけで分析をします。 また、説明変数には、質的変数と量的変数が混ざっていることもあります。 広義の数量化Ⅰ類 と 広義の数量化Ⅱ類 がこれに当たります。
数量化理論で扱われるデータの種類は、以下の４つに
分かれるようです。
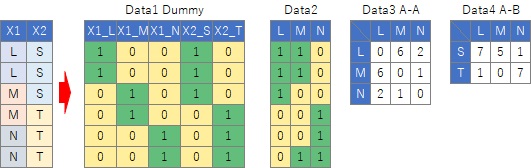
Data1とData2は似ていますが、「Lでなければ、MとNのどちらか」といった論理が必ず入っているかどうかが違います。
Data1の場合は、ダミー変換する前の形に逆変換して質的変数にできますが、Data2の場合はそれができません。
「数量化理論」の解説書は以下のようになっています。
Ⅰ～Ⅲ類は、質的変数や、０と１で「あり」と「なし」が表現されている変数を、量的変数の理論で扱う方法です。
Ⅳ～Ⅵ類は、 一対評価 で得られたデータから全体像を見るための方法です。
Ⅲ～Ⅵ類は、スタートになるデータの種類が異なるため、数学的な手続きが異なりますが、アウトプットが各カテゴリの座標データになる点は同じです。
オリジナルの数量化理論では、扱う手法がある程度の範囲に決まって来ます。 このサイトでは、下記の意味に広げて、その観点で書くことにしています。 こうすることで、もともと数量化理論でやりたかったことに対して、最新の理論を使ったアプローチが考えやすくなると思っています。
筆者は初めて数量化理論を知った時、「0と1のデータを扱うこと以外は、後は通常の多変量解析と同じ」という理解をしました。
ところが、この理解をしている内は、数量化理論でできることは限定されます。 数量化理論では、0と1になっているデータを扱うことによって、 どのようなモデルになっているのかを考えていくと、数量化理論ならではの分析の幅が広がりました。
上記のように、質的変数だけの時の数量化理論は、量的変数を対象としていた元の手法とは、わかることが異なる手法になります。
それだけでもデータ分析の世界が広がるのですが、 世の中の実際のデータには、量的変数と質的変数の両方がある時もあります。 両方がある時の進め方は、２種類あります。 これらを使い分けると、データ分析の世界はさらに広がります。
量的変数を質的変数で 層別 して分析する感じになります。
個々のカテゴリの相関分析 や 区間高次元化回帰分析 で使われている進め方です。
量的変数は質的変数になってから量的変数に戻るのですが、区分データとして扱われています。 非線形の特徴が見やすくなります。
「多変量解析法入門」 永田靖・棟近雅彦 共著 サイエンス社 2001
重回帰分析
、
判別分析
、
主成分分析
、
多次元尺度構成法
、
数量化Ⅰ～Ⅲ類 が体系的にまとまっています。
決定木
、
クラスター分析
についても短めにまとめられています。
「多変量解析がわかる」 涌井良幸、涌井貞美 著 技術評論社 2011
数ページずつですが、数量化１から４類と
コレスポンデンス分析
について、計算方法がコンパクトに解説されています。
各手法が何をどうやって数量化するのかが、わかりやすいです。
Ⅰ類：量的データを基準に質的データを数量化
Ⅱ類：質的データを基準に質的データを数量化
Ⅲ類：クロス集計表の表側と表頭のカテゴリーを数量化
Ⅳ類：互いの親近性から関係を数量化
コレスポンデンス分析：数量化Ⅲ類の拡張。クロス集計表で各セルに２以上の数字が入っている場合の方法
「数量化 理論と方法」 林知己夫 著 朝倉書店 1993
数量化理論の研究の歴史、Ⅰ類からⅥ類までの説明。多次元尺度構成法との関係
「数量化法の基礎」 岩坪秀一 著 朝倉書店 1987
数量化１～４類の計算式が詳しく書かれています。
３次元以上にデータを並べる、n-wayの数量化３類も詳しいです。
「質的データの数量化」 西里静彦 著 朝倉書店 1982
双対尺度法の本です。
双対尺度法というのは、計算方法は違うものの、やろうとしているのは数量化Ⅲ類や主成分分析と同じで、変数やサンプルの順番を解釈するための、
軸を見つける方法のようです。
順路
次は
広義の数量化Ⅰ類
