 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
多対多の分析
のA-B型は、データ処理の最初の段階がこの型になっている場合と、何らかの集計をして、この型にしている場合があります。
統計学の分野では、A-B型のAを「変数」、Bを「サンプル」として使う事が多いです。 そのようなデータについては、様々な分析方法があります。
変数の類似度の分析 や サンプルの類似度の分析 は、Aだけや、Bだけについての、その中での項目の類似度を見る分析です。
一方、A-B型の分析は、行と列の項目の、項目同士の類似度の分析です。
A-B型は、Aという見方の要素と、Bという見方の要素に、1対1の関係がある事を表してます。 A-B型の分析では、要素同士の1対1の関係を見て、AとBの関係を調べます。
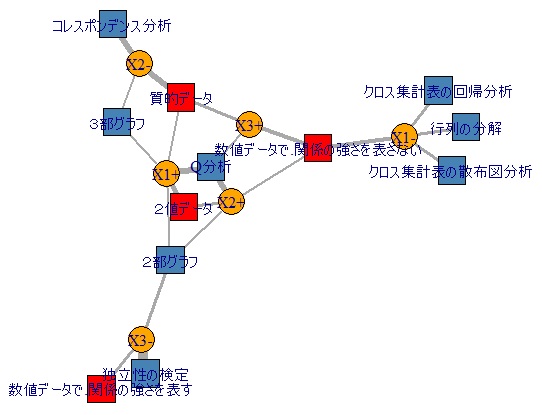
A-B型は、扱うデータの種類に違いがあります。
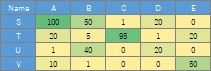 数値データで、関係の強さを表している場合
数値データで、関係の強さを表している場合
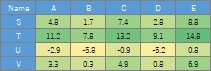 数値データで、関係の強さを表さない場合
数値データで、関係の強さを表さない場合
 質的データの場合
質的データの場合
データの種類によって、適した方法も異なります。
| 方法 | 数値データで、関係の強さを表す | 数値データで、関係の強さを表さない | 質的データ | 2値データ |
| 独立性の検定 | 〇 | × | × | × |
| クロス集計表の散布図分析 | 〇 | 〇 | × | × |
| クロス集計表の回帰分析 | 〇 | 〇 | × | × |
| 行列の分解 | 〇 | 〇 | × | × |
| 2部グラフ | 〇 | × | × | 〇 |
| 3部グラフ | 〇 | × | 〇 | 〇 |
| コレスポンデンス分析 | 〇 | × | 〇 | × |
| Q分析 | × | × | × | 〇 |
上の表は、〇と×しかないので、2値データのA-B型になっています。
2部グラフ
にすると、下のようになります。
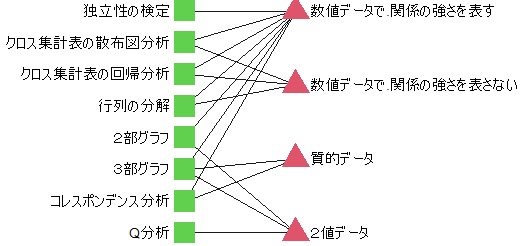
3部グラフ
にすると、下のようになります。
順路


 次は
クロス集計
次は
クロス集計

