左のような質的変数が２つあるデータがあったとします。 それをクロス集計 すると、右側のデータが作れます。
対数線形分析 には、 クロス集計 したデータの 回帰分析 という側面があります。
このように考えると、 A-B型の分析 として幅が広がります。
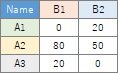
左のような質的変数が２つあるデータがあったとします。
それをクロス集計
すると、右側のデータが作れます。
クロス集計表の中でも、データの個数についてまとめたものは、 分割表 と呼ばれます。
対数線形分析
を実際に実行する時は、まず、
分割表を下のような形にします。
ダミー変換
します。
多重共線性
があるので、最終的に分析対象にするのは、下の形式のデータです。
目的変数が「Count」で、交互作用項 のある回帰分析をします。 このデータは、目的変数がカウントデータ（計数値）なので、普通の回帰分析ではなく、 ポアソン回帰分析 をします。
左のような質的変数が２つあるデータがあったとします。
今度はYという量的変数もあります。
Yの平均値（Average）で集計すると、右側のデータが作れます。
説明変数が質的変数の場合に、 ダミー変換 を使う回帰分析は、 数量化Ⅰ類 と呼ばれています。
ちなみに、上記は説明のために、X1とX2のそれぞれについてカテゴリが２つずつしかないですが、２つずつだと、サンプルが少な過ぎて分析が不安定になります。
場合分けとしては、クロス集計のデータが0と1だけの２値データの場合も考えられます。
２値データの場合は、 ロジスティック回帰分析 で何か出そうな気もしましたが、ダメでした。 クロス集計してしまうと、サンプル数が極端に少ない回帰分析になるのが原因のようです。
Rによるクロス集計表の回帰分析 があります。
R-EDA1 では、 行と列に項目名が配置されている 分割表 データのモデル化と、 変数の類似度の分析 の２つの使い道が、両方ともできるようになっています。
分割表のデータのモデル化は、
「Two_way_GLM」で、
「poisson_log」を選ぶとできます。
ちなみに、「gaussian_identity」を選ぶと、頻度のデータではない場合のモデル化で、数量化Ⅰ類になります。
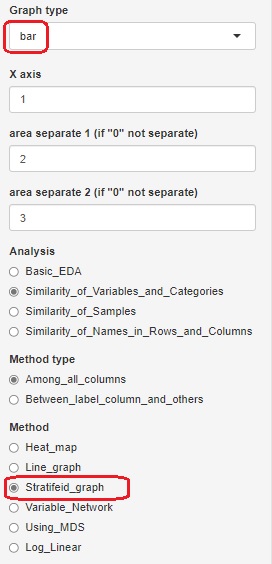
分割表に集計されていない質的変数のデータを使う場合は、やり方が２つあります。 「Method」で「Log＿Linear」を選ぶと、データセットの全部の変数をスタートにして、モデルの探索が始まります。 「Stratifeid_graph」を選んで、「Graph type」を「bar」にすると、グラフの作成に選んだ変数をスタートにして、モデルの探索が始まります。
この機能の場合、量的変数が混ざっていると、
量的変数は
１次元クラスタリング
をして質的変数として扱われます。
また、この例は、２変数ですが、３変数以上でもできます。
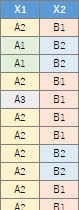
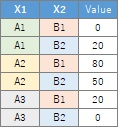
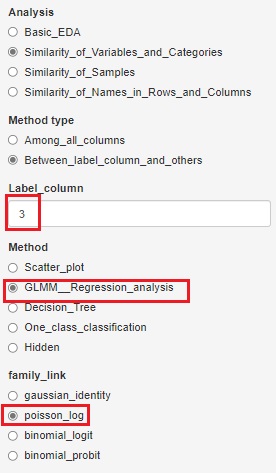
縦一列に数値が入っている分割表からスタートする場合は、一般化線形混合モデル（GLMM）の機能を選ぶとできます。
例の場合は、３列目に数値が入っているので、「３」を指定する必要があります。
この形の分割表になっていると、３変数以上でもできます。
順路
次は
行列の分解
