多変量解析 の手法では、YとXの 相関 の高さを調べようとします。 この時、X同士に相関がないと、すんなり解析できます。
しかし、 実験計画法 を使ったりして、意識して集めたデータでもない限り、 普通はX同士には相関があります。 解析に支障が出るほどX同士の相関が強い時に、「多重共線性（たじゅうきょうせんせい）がある。」、と言います。
多重共線性が大きな問題になるのは、データの背景（ メタ知識 ）を知らないで、 多変量解析 をする時が多いようです。
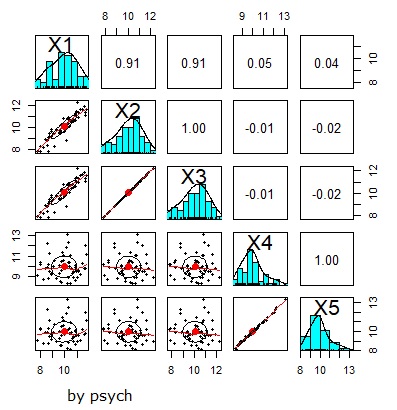
多重共線性の一番簡単な形は、 ２つのXの組についての 相関性 と同じです。 相関が非常に高い組合せがある場合は、多重共線性もあると言えます。
すべてのXの組合せについて、散布図や相関係数を見てみると、一番簡単な形の多重共線性はチェックできます。
この図は、Rのpsychを使っています。
Tokyo、LA、Paris、Londonの４つの名前があるため、
ダミー変換
の後に、４つの列がある例です。
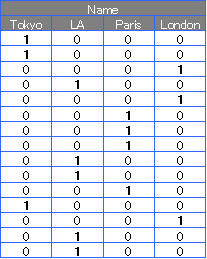
４つ列ができているのですが、 例えば、一番左の「Tokyo」の列がなくなると、４つの名前が表現できていないでしょうか？
実は、「LA」、「Paris」、「London」のすべての列が「0」になっていることでも、 「Tokyo」を表せているので、「Tokyo」の列はなくても大丈夫です。
別の見方をすれば、TokyoをYにして、LA、Paris、LondonをXにして 重回帰分析 をすると、寄与率が100%になります。 これは、他の３つの変数で「Tokyo」を表すという意味になります。
１つの列が、他の列の組み合わせで表現できる時も、多重共線性と言います。
多重共線性があるので、ダミー変換して作った変数をすべて使って解析をしようとすると、計算ができなくなります。
ダミー変数に限らず、一般的に、 あるXが、他の複数のXの 線形和 （重回帰式）で表せてしまう時に、「多重共線性がある」、といいます。
重回帰分析をして、寄与率が100%ちょうどにならなくても、それに近い時は「多重共線性がある」と言います。
多重共線性のチェック方法ですが、重回帰分析を全部の変数の組み合わせについて、計算するのは大変です。 この多重共線性のチェック方法としては、トレランス（tolerance）という尺度があります。 統計ソフトによっては、トレランスを計算してくれるものもあります。 トレランスが小さいと、多重共線性が起きていると考えられます。
ちなみに、一般的な多重共線性の定義には、２つのXの組の相関性と、ダミー変数の多重共線性の両方が含まれています。
筆者の経験の範囲になりますが、 「あるXが、複数のXの線形和になっている」、という現象を扱っているとしても、 データのばらつきが大きかったりすると、それを確認するのは難しいです。
一般的な多重共線性まで書きましたが、この知識が必要な解析はあまり出会いません。
完全な多重共線性が起きている時、つまり、 ある変数が他の変数の 線形和 で誤差なしで表せてしまう時は、 多変量解析 の計算の中で、計算できない部分（逆行列）ができてしまいます。
完全でなくても、それに近い場合は、解析結果が不安定になります。
多変量解析 で予測式を作る場合は、 多重共線性がある変数は、片方を解析の途中で取り除きます。
多重共線性があるという事は、数理的に区別できない変数があるという事なので、数理的にはこの対応方法で問題はないです。
例えば、２つの変数が多重共線の関係なら、片方の変数を取り除けば済みますが、 「どちらを除くべきか？」という問題があります。 解析結果の考察の時には、取り除いた方も、合わせて考える必要がありますが、 その時の考察でも苦労します。
多重共線性があると、回帰式が思うように作れなかったり、 多重共線性を除くのに苦労しますので、解説書等では、多重共線性を嫌っていることが多いです。
多変量の関係を式で表すのが解析の目的だったり、Yを予測する事が解析の目的だったりすると、 多重共線性は嫌な存在です。
しかし、解析の目的が、トラブルの原因を見つけたり、因果関係を調べたり、データの素性を調べたりする事でしたら、 多重共線性が見つかることは、むしろチャンスになる事があります。
変数の選択 の方法を駆使して、Xを絞り込むことはせずに、 「あるYの増減に対して、同じように増減するXが複数見つかり、しかも、それらのX同士に多重共線性がある。」、 というところがわかった所までで、解析は止めます。
次にやることは、多重共線性の関係になっている理由の調査です。 複数のXが同じような変動をする時には、それらのXに共通の因子があると考えられます。 多重共線性の関係は、その因子を見つけるための手がかりになります。 因果推論では、その因子がわかった時点で、解析は完了する事もあります。
順路
次は
主成分回帰分析
