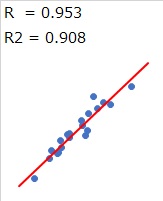
２つの項目のデータを ２次元散布図 にプロット（打点）した時に、 ほぼ”直線状”にプロットが並ぶ場合、「相関（コリレーション）がある」と言います。 「相関が強い」とか、「相関性が高い」とも言われます。
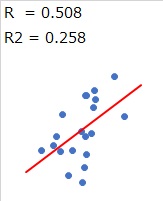
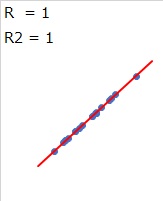
相関性を評価する尺度が「相関係数（R）」です。 相関係数が＋１や−１なら、プロットは完全に直線状になっています。 ０に近いほどばらつきます。 相関係数は ばらつきの尺度 の一種です。
相関係数が＋１や−１に近い時は、「相関がある」と言います。
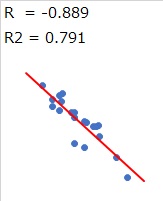
＋１の場合は「正の相関」、−１の場合は「負の相関」と言います。
「相関がある」の基準は、
実際のデータや解析の意味を考えて、ケースバイケースで考える必要があります。
解説書では、例えば、「0.7 以上」と書かれていることもあります。
これは考える時の目安になります。
単回帰分析 のページにあるように、相関係数の２乗には、寄与率としての使い方があります。
寄与率が0.5（50%）だとすれば、「２つの項目には直線的な関係で、２つの項目の値が決まっている」という要因で説明できるのが、0.5という意味になります。 0.5は、ちょうど半分なので、目安として便利です。
0.7の２乗は、0.49で約0.5です。 つまり、相関係数を0.7で目安にするということは、寄与率が0.5を目安にすることと、ほぼ同じです。
このように、目安が0.6や0.8でなく、0.7であることには、それなりに意味があるようです。
ちなみに、0.6や0.8を使う時は、以下の意味として考えると良いかもしれません。
実際のデータ解析で使うデータは、必ずしも等間隔ではなく、 データの密集している部分や希薄な部分があったり、分布があります。 Excel等で試してみるとわかりますが、 相関係数は、分布の外側のプロットの影響が大きいです。
入力間違い等の 外れ値 によって、相関係数が±１に近くなってしまうことはあり得ます。 そのため、「相関がある。」という結論を出す場合は、 散布図 を描いてみるなりして、妥当なデータを使用しているかのチェックが必要です。
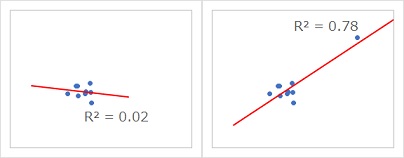
例えば、下の左右のグラフは、右上の１点の有無だけが違います。
しかし、離れたところにこの１点があることによって、相関係数がだいぶ違います。
順路
次は
相関係数で見える事と見えない事
