このサイトでは、いくつかのページで寄与率が出て来ます。 元になっている計算方法は、 分散分析 や 平方和分析 ですが、意味合いがだいぶ違っています。
このページは、そうした違いについてまとめたものです。
寄与率が計算できると、「この原因が、全体の５割に影響しています」といった分析ができるようになります。 思い込みの対策 をさけるための 要因解析のためのデータサイエンス として、とても頼りになる技です。
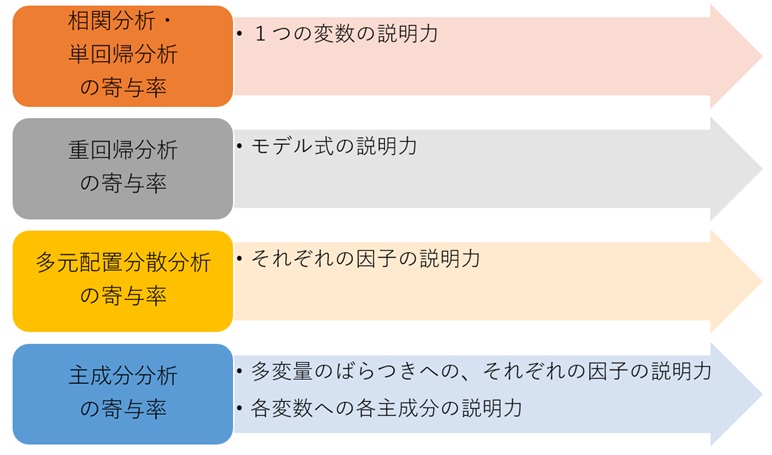
相関分析 や 単回帰分析 では、２つの量的変数の関係をみます。
これらの分析における寄与率は、片方の変数による、もう片方の変数の説明力を表します。
より正確には、直線的な式で近似できると考えた時に、その式の説明力を表します。
寄与率は、２つの量的変数の、相関係数の２乗で計算できます。 平方和の比でも計算できます。
二値データの寄与率 のページに詳しくまとめましたが、相関分析の寄与率は、連続データでなくても役に立ちます。
重回帰分析 では、複数の変数を使ってモデル式を作ります。 式ができれば、予測値を計算することができます。
寄与率は、予測値と実測値の、相関係数の２乗で計算できます。 平方和の比でも計算できます。
この方法は、 重回帰分析 に限らず、量的変数のモデル式を作る方法なら、何でも使えます。
予測値の精度が高ければ、予測値と実測値は直線状にデータが並ぶ性質を使っています。
多元配置分散分析 では、目的変数が量的変数で、説明変数が質的変数です。
寄与率は、それぞれの質的変数の説明力を見る指標になります。
ただし、この方法は、「目的変数が量的変数で、説明変数が質的変数」ならどんなデータでも使えるわけではないです。 実験計画法 を使って、各変数が独立するように、計画的に集めたデータの場合に使える方法です。
主成分分析 には、寄与率として求められるものがひとつと、寄与率そのものではないけれども、寄与率として使えるものの２種類があります。
多変量データのばらつき方について、全体のばらつきに対して、その主成分でどれだけ説明できるのかを見ます。 例えば、「第１主成分までの寄与率は40%」といった使い方をします。
主成分分析では、第１主成分が一番寄与率が高くなります。 累積寄与率というものもあり、 例えば、「第３主成分までの累積寄与率は90%」といった場合は、第１から第３までの主成分で、全体のばらつきをどれだけ説明できるのかを表します。
主成分分析では、「因子負荷量」というものが計算されます。 因子負荷量は、例えば、X1という変数があった時に、X1と、主成分PC1の相関係数です。
因子負荷量の２乗は、相関係数の２乗なので、寄与率として使えます。
重回帰分析の寄与率は、モデル式の説明力を表します。
多元配置分散分析の寄与率は、説明変数が質的変数の時に、それぞれの質的変数の説明力を表します。
主成分分析の寄与率は、主成分という量的変数について、それぞれの説明力を表します。
そうすると、重回帰分析の時に、それぞれの説明変数について、説明力を調べたくなりますが、 一般的には、それを調べる方法はないです。 このあたりの事情は、 個別の因子の寄与率 にあります。
順路
次は
個別の因子の寄与率
