要因解析のためのデータサイエンス

要因解析の時のデータサイエンスは、現状把握のためのデータサイエンスで調べた結果系のデータに対して、「変化のタイミングが似ているもの」や、「増減の仕方が似ているもの」をデータから調べます。

要因解析は、仮説の探索と、仮説の検証に大きく分かれますが、データサイエンスを使う場面も、それらに対して使うものが変わります。

仮説の探索のためのデータサイエンス

従来からよく使われて来た手法は、なぜなぜ分析、連関図、特性要因図といった定性的な仮説の探索です。

21世紀に入ったくらいから、データサイエンスは定量的な仮説の探索の方法としても大きな貢献ができるようになって来ています。

テーブルデータ（表形式のデータ）を調べる場合、変数が少ない場合は、２次元散布図を使って行けば良いです。

変数が多いと、２つの変数の組合せを無数に見ることになり、大変です。

変数の類似度の分析や、カテゴリの類似度の分析をすると、全体的な関係がわかりやすくなります。

また、使う機会はあまりないですが、データサイエンスならではの分析方法として、隠れ変数の探索というものもあります。

これらの方法の中では、多変量解析や機械学習のモデルを使いますが、精度の高い推論モデル（予測モデル）を作ることが目的ではないです。

データの構造を調べるために使っています。ちなみに、「データの構造を調べるために、多変量解析や機械学習のモデル使う」という使い方は、一般的にはあまり紹介されません。

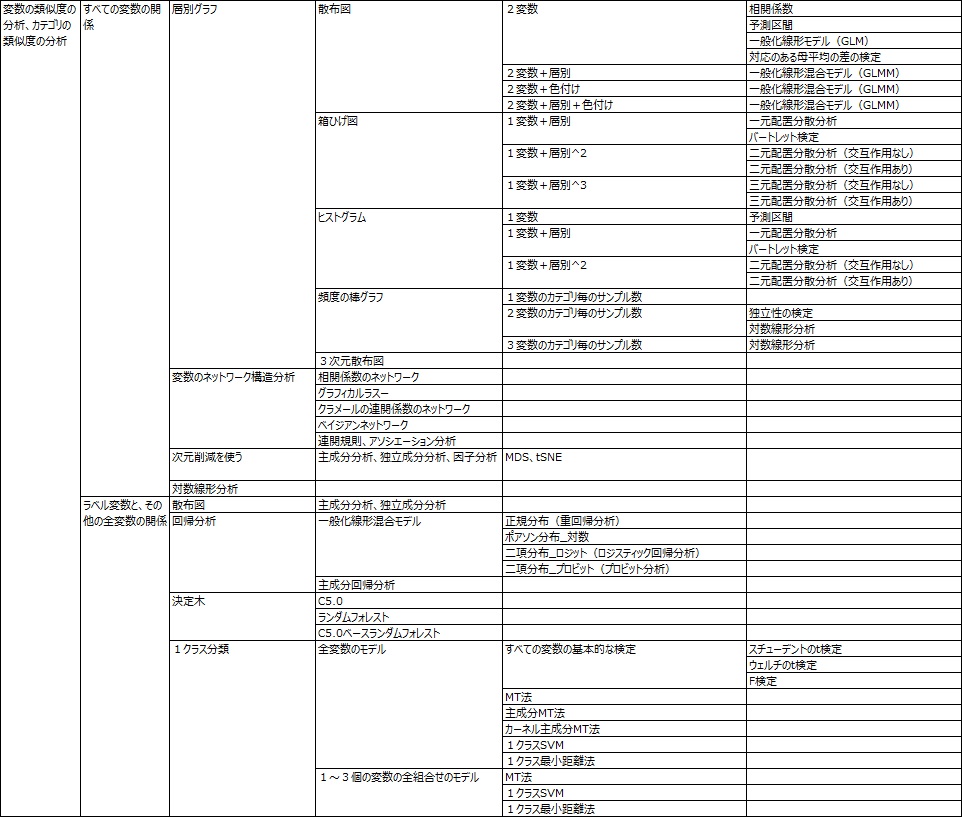
R-EDA1 の「Similarity_of_Variables_and_Categories」には、モデルとグラフを組み合わせた、様々な分析のレシピを入れました。

要因解析のためのデータサイエンスに使えるソフトで、これほど多くのレシピが入っているものは、他にないと思います。
ウェブアプリ　R-EDA1

因果推論の理論の中には、データだけから因果関係の結論を導き出そうとするものもあります。統計的因果推論と呼ばれています。

事実と反事実の分析とまではいかないまでも、「反事実のデータがあったとしても、結論は同じと言えそうか？」という確認は役に立ちます。

統計的因果推論には、持っているデータだけから、仮説の検証を完結させようとする性格があります。

一方、持っているデータだけから仮説の検証まで完了させようとするよりも、簡単な実験をしてみたり、対策の実施を少しやって仮説の正しさを確認する方が、はるかに早く、確実に仮説を検証できることが多いです。

そのため、統計的因果推論とバランスを取りながら進めると良いです。

要因解析の中では、仮説の探索や検証のために、実際に実験をしてみると良いことがあります。

実験自体はデータサイエンスではないですが、効率良く実験をするためには実験計画法を知っていた方が良いです。また、実験データのばらつきを考察するには、誤差の知識もあった方が良いです。これらがデータサイエンスです。

実際の実験ではなく、コンピュータの中で実験する方法として、シミュレーションがあります。

シミュレーションでは、使うモデルが多変量解析や機械学習のモデルの時があります。

数理モデリングとして、物理法則などをモデルにする時も、データの準備や結果の解釈で、データサイエンスの知識が役に立ちます。

実験計画法のデータ分析では、因子ごとに寄与率を出すことができます。例えば、「因子Aで、全体の５割が決まっている」という分析ができます。

実験データがない場合、例えば、特性要因図で洗い出した因子に対して、寄与率を求めることは普通はできません。

しかし、要因が複数ある場合は、フェルミ推定のようなざっくりした方法でも良いので、寄与率を見積もった方が良いです。思い込みで対策してしまう原因として、象徴的な出来事を唯一の原因のように思い込んでしまう話がありますが、そうした間違った考察を防止することができます。

製造業の品質問題などでは、誤差（ばらつき）の分析が必要になります。しかし、誤差は実感がわきにくく、分析しにくいです。

ちなみに、誤差因子のようにして、実験的に発生させて分析することもあります。

誤差の理論は、データサイエンスとしてメジャーではないですが、誤差を的確に分解したり、定量化できたりすると、要因解析としては大成功になります。筆者自身は、数理モデリングと誤差の伝播を組み合わせたり、二重測定による繰り返し誤差の推定を使って、誤差について、仮説の探索と検証をしたことがあります。