二重測定による繰り返し誤差の推定

測定の誤差を知りたい時は、同じものを何度も測って標準偏差を求めるのが、一番確実です。

しかし、同じものを測ることが難しかったり、手元にあるデータだけで、どの程度なのかだけでも知りたいことがあります。そのような時に、二重測定のデータは役に立ちます。

サンプルのばらつきと、繰り返し誤差の区別から

測定器Aと測定器Bで、5つのサンプルを測ったデータがあるとします。それぞれの標準偏差が求まります。
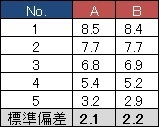
対応のある場合のデータ

Aが2.1、Bが2.2という標準偏差になっていますが、この値は、サンプルのばらつきと、繰り返し誤差が合わさった値です。式で書くと、下のようになります。
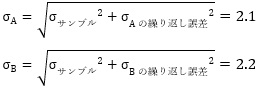
対応のある場合のデータ

5つのサンプルは、だいたい3～8までの値を均等に分けるような値のサンプルで、 AとBの対応する測定値の差は、大きくても0.3なので、2.1や2.2という標準偏差の大部分は、サンプルのばらつきが占めていることは推測できますが、これだけではどうしようもありません。

上の2つの式をそれぞれ２乗します。
対応のある場合のデータ
すると、同じ項があるので、これが打ち消し合うように、2つの式を引くと、AとBの繰り返し誤差の差は求まります。

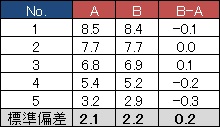
対応のある検定と同じように、AとBの差を計算します。そして、この差の値の標準偏差を計算します。
対応のある場合のデータ

誤差の伝播にもありますが、この差の標準偏差の意味は、
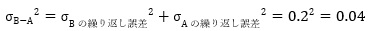
対応のある場合のデータ
になります。

ここまで来ると、ゴールが見えてきます。繰り返し誤差の和と差がありますので、連立方程式になって、同じサンプルを同じ測定器で繰り返し測定をしていないのに、繰り返し誤差が求まってしまいます。
対応のある場合のデータ

このページの計算には、注意点がひとつあります。このページでは、計算を理解しやすいように、n = 5　になっていますが、誤差とn数にあるように、n = 5 というのは、誤差の大小を評価するには少ないです。 n = 5だと、ある程度の目安くらいにしかなりません。