二重測定による判別能力の向上

下のような散布図があったとします。青い丸のプロットが、正常時のデータとします。赤い三角のプロットは、正常か異常かわからないデータとします。

赤い三角のプロットは、青い丸のプロットの範囲に入っているので、「赤い三角のプロットは正常」という判定がされる場合が、一般的には多いと思います。ただし、検定を知っている人は、範囲の端の方であることを考えて、「異常かも」と迷うかもしれません。
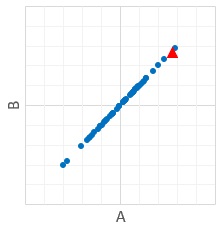
対応のある場合のデータ

ところで、このような場合は、 AやBの片方の変数だけでできる判定と、両方合わせてできる判定が変わらないので、変数が２つある事には利点がありません。

筆者の経験の範囲になりますが、たくさんの変数（項目）のデータがあっても、重要な変数同士には多重共線性の関係があって、上の図のような状況になっていることがほとんどです。

このページのこの後は、上の図のような状況ではない時の話です。知っていると、出会った時に役に立ちます。

なお、このページの話は、相関性の考え方の話なので、二重測定のデータに限ったものはないです。ただ、現実に起こりがちなのは、二重測定のデータのようです。

二重測定をしていると、判定に確信が持てるパターン

下のような散布図があったとします。上の散布図と比べると、赤い三角のプロットの位置は同じですが、青い丸のプロットは全然違っています。
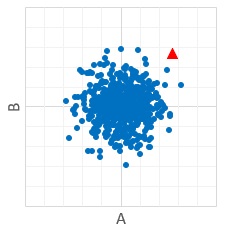
対応のある場合のデータ

赤い三角のプロットの位置は、Aの方向で考えても、Bの方向で考えても、青い丸のプロットの範囲に入っています。そのため、この場合も「赤い三角のプロットは正常」という判定ができそうですが、この図の場合は、事情が違っています。

ポイントは、AとBに相関がないことです。相関がないということは、Aの方向で見た時に範囲の端の方であったとしても、Bの方向で見た時にどこにあるのかは無関係ということになります。

そのため、AとBの両方で範囲の端の方で発生するということは、ただごとではない事が起きているという事を意味します。 AやBの両方に対して、範囲の中になっていても、「これは異常の可能性が高い」という判定をすることができます。

二重測定（対応のあるデータ）の使い道として、ひとつの測定では判別が難しくても、２つの測定の両方の結果を合わせることで、判別能力を向上させられることがあります。

散布図の見た目ではなく、定量的に判定する方法としては、 MT法や決定木があります。これらの手法を使うと、「起きにくいことが二重に起きているということは、ものすごく起きにくいことが起きている」ということを、定量的に扱えます。

AとBに相関がある場合、Aで範囲の端の方になる時は、Bでも範囲の端の方になるのが当たり前なので、相関がない時のような分析の仕方ができません。

ふたたび、下のようにAとBが完全に相関している場合を考えます。 AとBが完全に相関している場合には、二重測定でなければ絶対にわからない異常のパターンがあります。それが、下の図の緑色の四角のプロットの位置です。
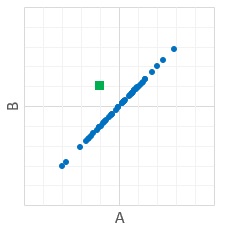
対応のある場合のデータ

AとBのどちらか一方を見る限りでは、どちらを見たとしても、正常値の範囲の中心付近にありますので、この点が異常値だとは、絶対に思えません。

<相関関係がない時の探索のページに、ふだんは相関しているのに相関しないことに注目する話がありますが、それと似ています。

MT法は、多重共線性のあるデータには使えないため、２つの変数が完全に相関している場合は、使えません。

しかし、ある程度は相関しているとしても、相関係数が±1にはなっていないのでしたら、 MT法は、二重測定のデータの検証に役に立ちます。

完全に相関している場合には、単回帰分析をして、予測値と実測値の差の大きさで考えた方が良いかもしれません。