MT法のM と T とは、マハラノビス氏の M と、 品質工学 で有名な田口玄一氏の T です。
判別分析 が典型的ですが、 パターン認識 の方法の多くは、「AとBの、どちらなのか？」、という分析に使われます。
こうした方法は、「AとB」が、「野菜と果物」や、「１グループと２グループ」のような分類のものを分析する時には、あまり問題がないです。
ところが、「AとB」が「正常と異常」の時には、こうした方法の数理では、うまく分析できない事があります。 「正常と異常」の原因分析や、「正常と異常」の判定や予測には、こうした方法は不向きな事があります。
MT法は「正常と異常」を、うまく分析できる数理になっています。
「異常」というと、機械の異常がイメージされる事が多いかもしれませんが、 品質学 の分野での「正常と異常」には、「良品と不良品」もあります。
MT法が「異常」を扱うのに適している理由は、判別分析と比べると、わかりやすいかと思います。
判別分析の場合、判定不明なサンプルは、まず、「正常」と「異常」の両方のグループの中心からの距離を測ります。 次に、「どちらのグループに近いのか？」と考えて判定します。
図の場合、「正常」側からの方が短いので、判別分析では「正常」と判定されます。
MT法の場合は、まず、「正常」の中心からの距離だけを測ります。 次に、「正常なら、距離はこのくらいの範囲。これより長いのなら異常」と考えます。 検定 の考え方と似ています。
図の場合、MT法では「異常」と判定されます。
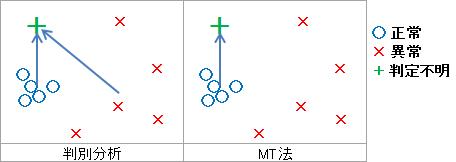
MT法では、「正常でなければ、異常」と考えますので、モデル作りで、異常のサンプルのデータは必須ではありません。
ただし、異常のサンプルのデータは、異常の 原因解析 をする時には、もちろん必要です。 また、「異常」とわかっているサンプルが「正常」と判定されるモデルでは、お話になりませんので、モデルの妥当性の確認に使うこともあります。
MT法は、もともと 品質工学 の中の MTシステム の手法として1980年代に考案されたものです。 しかし、その数理は、品質の分野だけで役に立つ方法という訳ではなく、汎用性が高いです。
2010年代になってからは、 異常のモデル として、品質の分野以外でも取り上げられる事が多くなっています。 実際のところ、MT法は、 機械学習 の分野でいうところの 1クラスモデル と同じ手順を使っています。
Yが量的変数の時はT法で、質的変数の時はMT法を使えば良いのですか？
「標準化と品質管理 Vol.170」 日本規格協会 2017
MTシステム
の特集が組まれています。
手島昌一氏と田村希志臣氏の共著で、MT法と
ディープラーニング
（深層学習）を比較している記事があります。
MT法は、1つの状態を学習して、その状態か否かを調べる方法として紹介し、
ディープラーニングは、複数の状態を学習する方法として紹介しています。
これらの使い分けや融合で大きな成果が出ることを提唱しています。
「MTシステム解析法入門 試して究める!品質工学」 鈴木真人 著 日刊工業新聞社 2012
解説が平易です。
この本の特長は、無償でダウンロードして、MT法、T法、RT法を実施することのできるExcelベースのソフトが用意されていることです。
MT法の事例は、要因解析があります。
「入門 MTシステム」 立林和夫 著 日科技連 2008
文字や波形データのパターン認識の話が詳しいです。
水準を複数作って、それを通過するポイントを中間データとして集計して、その中間データについてMT法で分析しています。
マルチ法も紹介されています。
「よくわかるMTシステム ：品質工学によるパターン認識の新技術」 田村希志臣 著 日本規格協会 2009
MT法の事例は、要因解析があります。
この本の事例は、信号空間のデータ全部に共通する要因解析ではなく、個々のデータについての要因解析をしています。
また、この本は、
マルチMT法
のやり方が詳しく書かれています。
「コンピュータによる情報設計の技術開発 シミュレーションとMTシステム」 矢野宏 編 日本規格協会 2004
レース車の異常検知の事例があります。
その他は、マハラノビス距離を指標にする話もあります。
「MTシステムにおける技術開発」 兼高達弐 編 日本規格協会 2002
事例が非常に豊富です。
変数の選択をして、変数を絞って異常を判定するシステムを作ろうとしている事例が多いです。
「おはなしMT（マハラノビス・タグチ）システム」 鴨下隆志・矢野耕也・高田圭・高橋和仁 著 日本規格協会 2004
「MTシステムにおける技術開発」の内容を、「おはなし」としてかみ砕いて説明している感じの本です。
マルチ法が紹介されています。
「品質を獲得する技術」 宮川雅巳 著 日科技連 2000
判別分析
との比較をしています。
順路
次は
単位空間
