データサイエンスの数理

データサイエンスでは、手法の使い道（目的）と、手法の内容のつながりを考えながら使い分ける事が大事なのですが、とてもわかりにくいです。

手法と目的の関係は、一対一や、一対多ではなく、多対多です。これが、全体像の理解を難しくしているようです。

特に数理モデルはわかりにくいので、このページでまとめてみました。

手法と目的の関係

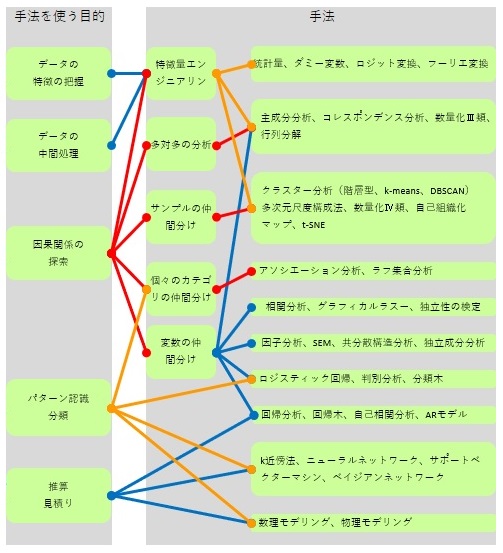
手法と目的の関係は、図のような感じです。

因果関係の探索（因果推論）にモデルを使う場合は、モデルの構築の段階で気付いた事が重要です。データとして持っていない事実にも気付く事があります。そのため、できた式に含まれる変数や、式の精度はあまり重要ではありません。

「予測・判別」に数理モデルを使う場合は、できた式に値を入力することによって、予測や判別をします。式の精度（予測精度、的中率、等）は、非常に重要になります。

データ分析の教科書にあるような方法には、コンピュータが手軽に使えない時代に考案され、コンピュータの普及とともに、一般人でも手軽に使えるようになったものが、数多くあります。

コンピュータの普及直後くらいまでは、一般の人が使うデータは、行も列も大したことがないので、あまり議論されなかったようですが、現代において、教科書にあるような方法を、教科書通りに使うと問題が起きたり、期待したことができないことがあります。

主成分分析やコレスポンデンス分析は、分析結果を見る時に散布図にして、「これとこれは近い」といった分析をします。

変数が少なく、近い同士のグループが２、３個になるデータに対しての分析だとこれで十分なのですが、ある程度の規模になると、このやり方では見逃しや間違いが起きます。

この原因ですが、散布図で見るということは、２次元で表現できることを見ています。データの規模が大きくなると、分析結果が３次元以上になっていて、ある２次元で見ると近くに見えていても、実は他の次元ではとても遠い、という現象が起きます。

この問題の解決方法ですが、比較的簡単なのは、２次元の組み合わせの散布図をいろいろ作って、総合的に考える方法です。しかし、この方法では、グラフが２枚以上できてしまうため、意思決定をするのが難しいです。

グラフを１枚にまとめる方法としては、高次元を２次元に圧縮して可視化の方法があります。ただし、この方法では、主成分分析やコレスポンデンス分析自体の敷居の高さに加えて、２次元に圧縮する方法の敷居の高さが加わりますので、「このグラフは何なのだ」という話になりやすいと思います。

手順は明らかにして、「多次元で見た時に距離が近いものが近くに配置されるように散布図が作られています。散布図の縦軸、横軸の数値には特別な意味はありません。」という説明をして、意思決定の資料としての正しさを確保する進め方をするのがベストのようです。

ところで、高次元を２次元に圧縮して可視化の方法は、もともとサンプルの類似度の分析の方法として、よく知られているものです。

変数の類似度の分析、高次元を２次元に圧縮して可視化、サンプルの類似度の分析のそれぞれの方法は、よく知られているものですが、組み合わせると単独ではできなかった分析ができるようになるのがポイントです。

Rによるデータ分析は、このようなことを考えて、組み合わせた場合のサンプルコードが多くなっています。

統計学の分野では、「因果推論」という分野がかなり昔からあります。

「相関関係は因果関係ではない」といった話題がありますが、この分野での議論は伝統的に変数の関係を調べる方法です。暗黙の内に、「現象の中にある因果関係を明らかにする」という目的が「変数の数理的な構造を明らかにする」という話に置き換わって解説されているのが一般的です。

しかし、この方法は、現実の問題を解決するには厳しいものがあります。

その原因のひとつは、現実の問題で扱うデータは、バイアスだらけ、誤差だらけな点にあります。また、「『原因＝データの中の何か』と本当に言えるのか？」、という根本的な不明点もあります。

このようなデータに、変数の関係を見る手法をいくら使っても、何もわからないことになります。こんな時は、個々のカテゴリの類似度の分析をして、データがどのようになっているのかを把握していくことで、因果関係を究明する突破口になることがあります。

時系列解析のページに詳しく書いていますが、伝統的な時系列解析は、自己相関分析の理論が中心になっています。

そのため、「この現象は時間的な変化が重要だから、時系列解析」と思って、伝統的な時系列解析の解説を読むと、知りたいこととのギャップがあります。