判別分析 、 ロジスティック回帰分析 、 MT法 、 決定木 、 サポートベクターマシン は、目的変数Yがカテゴリデータになっている点が同じです。
解析の目的と、扱うデータによっては、同じ結果になることもありますが、 データの分布の仕方によっては、適さない手法を使ってしまうことがあります。
Yがどのようなデータであるのかとか、解析の目的でこれらの手法の使い方を説明することもできますが、 これらの手法が役に立つ場面を簡単な図にまとめてみました。 相関関係の探索 を目的にして、これらの手法を使う時には、特に重要な知識になります。
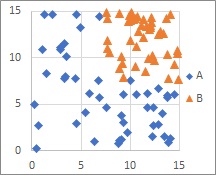
図は、YがAとBの２つで、説明変数が２つの場合です。
2つ以上の塊がある分布は、どの方法でも得意です。
距離による判別分析 は、2つ以上の塊がある分布に適しています。 それ以外は不得意です。
距離による判別分析では、それぞれの塊の中心からの距離を見ます。 線による判別分析では、この塊を分けるための境界線（正確には、境界超平面？）を探します。
ちなみに、
決定木
も境界を探しますが、ひとつの式で表せるような境界ではないです。
ロジスティック回帰分析
や
MT法
は、境界を探しません。
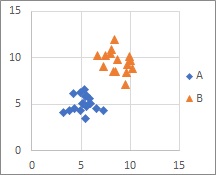
どの方法でも扱える分布は、カテゴリごとにサンプルが塊になっているような分布です。 サポートベクターマシン 、 ロジスティック回帰分析 、 決定木 は、塊がなく、空間にサンプルが散らばっていて、散らばり方に偏りがあるような分布でも扱えます。
サポートベクターマシン は境界線が引ける辺りのサンプルだけを見るので、異なるカテゴリのサンプルが集まっている必要はありません。
ただし、ロジスティック回帰分析と違って、境界線を引こうとする方法なので、境界線らしいものがないような混ざり方をしている時は、適さないです。
具体的には、片方のデータ群の表れ方が0.5以上の領域がないと、エラーになります。
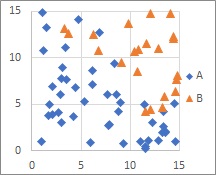
サポートベクターマシン の得意な分布は、 ロジスティック回帰分析 も得意です。 さらに、 ロジスティック回帰分析 では、異なるカテゴリのサンプルは、だいたい分かれていたり、出方に偏りがあるものの、境界線らしいものがない混ざり方をしている時も得意です。
ロジスティック回帰分析は、「だいたい」というのを、確率を使って数値で表現できます。
例えば、ほとんどの領域でＡの発生率が０で、一部の領域で最大で発生率が0.1になるような分布をしている場合、
ラベル分類
では、判別結果はすべてBになります。
多くの手法は、それ以上はわからないのですが、ロジスティック回帰分析では、低い確率を扱うモデルを作れます
例えば、左のようにBはAに比べて相当多く、偏りはなそうなものの、Aは左下に偏っているような時に、ロジスティック回帰分析では右図のような分析ができます。
この場合は、Bの割合がわかります。
一番Bが少ないところで、0.6くらいです。
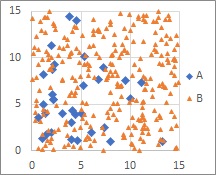
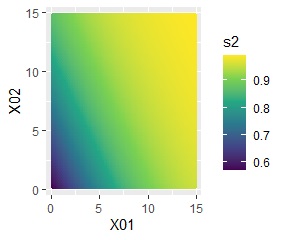
決定木 は、各軸に垂直に境界線を引いて行くので、各軸に垂直にデータが集まっていると、精度良く分割します。
各軸に垂直ではない線が、境界線になっている場合、垂直な境界線の組合せで近似するので、モデルが複雑になります。
空間の向きを変えるとシンプルに分割できるのに、
複雑な分割（モデル）になることがあります。
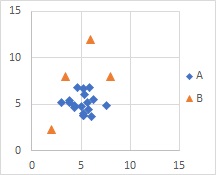
MT法 、 混合分布MT法 、 1クラス最小距離法 は、ひとつのカテゴリについては塊があって、塊になっていないカテゴリがあっても扱えます。
MT法 では、Aが集まっています。 正規分布を仮定しています。 MT法では、この群を 単位空間 と呼んでいます。
Bには、集まっていることや、正規分布の仮定がありません。 Bは、信号空間と呼びます。
MT法では、Bのサンプルの数が、モデルの精度に影響しません。１個でもモデルが作れます。
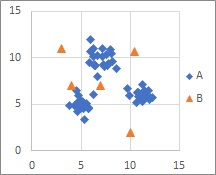
混合分布MT法
は、正規分布が複数あるような分布の時に適しています。
1クラス最小距離法
は、Aのサンプルの集まりがあって、Bが離れているような時に適しています。
Aの形は何でも良いです。
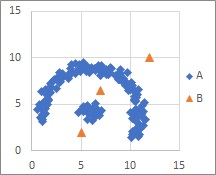
このページの例になっている分布は、わりとシンプルです。
もっと複雑になって来ると、まず、 MT法 では対応しきれなくなります。 決定木 で、ある程度の解析ができます。
判別分析、 ロジスティック回帰分析、 サポートベクターマシン については、 カーネル法 を追加することで、対応できるようになります。 ただし、カーネル法を使うとしても、AとBの境目があいまいなものは、判別分析や、サポートベクターマシンには不向きです。
ニューラルネットワーク や、 k近傍法 は、分布が複雑でも、境目があいまいでも、対応できます。 ただ、「対応できる」といっても、これらの手法には、結果の解釈の難しさや、精度の問題が出て来ます。
順路
次は
手法による結果の違い
