混合分布MT法は、 クラスター分析による予測 の方法です。
単位空間 （学習用データ）が、正規分布が複数重ね合わさっているような混合分布の時に使える方法です。
MT法 や 主成分MT法 は、正規分布を前提にした理論なので、データに合わない事があります。 この対策として、 カーネル主成分MT法 や、 One-Class SVM がありますが、これらはパラメータの調整が難しく、また、うまく調整できたとしても、精度が良くなかったりします。 混合分布MT法は、これらの方法ほどの万能さはないのですが、扱いやすさや精度は、これらよりもずっと良いです。
なお、「混合分布MT法」は筆者の造語です。 この方法について、公式な文献があればその名前に合わせたいのですが、さしあたって見つかっていないのでこの名前にしています。
例えば、下のような散布図のデータがあったとします。
赤いプロットの「0」は、２つのグループに分かれていて、青いプロットの「1」は４つあり、いずれも２つのグループの両方から離れたところにあります。
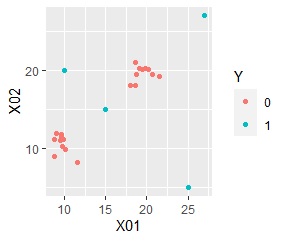
「0」を単位空間として混合分布MT法で分析すると、以下になります。
「1」の点が２つのグループの両方からどのくらい離れているのかが、定量的に示すことができています。
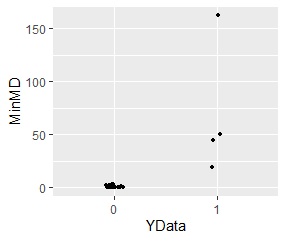
混合分布MT法では、単位空間に対して、まず、個々の正規分布の部分に分解します。 この分解には、 クラスター分析 の中でも、混合分布法を使います。 なお、k-Means法でも似たことができます。
次に、個々の正規分布に対して、 マハラノビスの距離 を計算します。 マハラノビス距離の定義は、MT法で使われている変数の数で割るものを使います。 MT法の定義では、変数の数が違っても、同じしきい値（判定基準の数字）を目安にできます。
こうして、ひとつのサンプルについては、複数の正規分布からのマハラノビス距離が求まります。
この複数のマハラノビス距離の最小のものがある正規分布が、 そのサンプルが属している正規分布として判断します。 また、最小のマハラノビス距離が 単位空間 （学習用データ）のマハラノビス距離の分布よりも大きく外れているようなら、そのサンプルは外れ値と判断します。
ところで、上記のアルゴリズムの中で、最初にクラスター分析をして、個々の正規分布に分解する手順の後は、 判別分析 で距離を使って判別する方法と、ほぼ同じです。
「まったく同じ」ではなく、「ほぼ同じ」なのは、 マハラノビスの距離 の定義式が少し違う点と、結果として求めようとしているのが、「どの正規分布に属しているか？」が判別分析なのに対して、混合分布MT法では、 「一番近い正規分布からどのくらい離れているか？」を見ようとする点です。
ちなみに、判別分析と混合分布MT法で、マハラノビス距離の定義式を入れ替えたり、見ようとするものを入れ替える使い方もできます。
手法による得意な分布の違い のページに、 判別分析 と MT法 の違いがあり、両者は異なるものとして説明しています。 ややこしいのですが、混合分布MT法では前処理にクラスター分析を入れることで、 判別分析 の一種でもあり、 MT法 の一種でもある方法になっています。
Rの実施例は、 Rによる混合分布MT法 のページにあります。
順路
次は
MT法による異常の判定
