混合分布MT法 は、 クラスター外の予測の分析 の一種です。 MT法 の応用と、 クラスター分析による予測 の応用の、２つの特徴があります。
一般的なMT法は、 RによるMT法 のページがあります。
このページのコードは、入力データに「Y」という名前の変数が入っていることを想定しています。
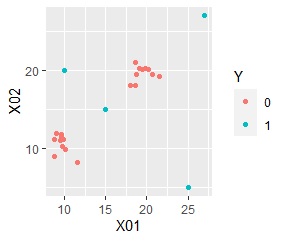
「Y」の変数は、「0」と「1」の２つの数値が入っていることを想定しています。 「0」のサンプルは、単位空間であることを想定しています。 「0」のサンプルだけでモデルが作られます。
「1」のサンプルは信号空間です。 単位空間のデータに対して、異常なのかを見たいデータになります。
Y以外の変数は、名前に決まりはありません。
計算結果はグラフになるようにしましたが、定量的な結果として、誤判別になるサンプル数がわかるようにもしてみました。 最後に出てくる数値がそれです。
混合分布MT法
は、多次元正規分布が複数あるデータが、単位空間になっている時の方法です。
クラスター分析
でグループに分けてから、それぞれに対してMDを計算して、各サンプルはMDの最小値（一番近いグループとのMD）を出力します。
library(ggplot2) # ライブラリを読み込み
library(mclust) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data# 質的変数がある場合にこの行を差し替え
Data2 <- subset(Data1, Data1$Y == 0)# Yが0のサンプルのデータを別に作る
Data2$Y <- NULL # Yの列を消す
YData <- Data1$Y# Yの列を別にしておく
Data4<- as.data.frame(YData)
Data1$Y <- NULL # Yの列を消す
k <- ncol(Data2) # 変数の数を計算
kNumber <- 2 #クラスターの数を指定
mc <- Mclust(Data2,kNumber) # 混合分布で分類
output <- mc$classification # 分類結果の抽出
Data3 <- cbind(Data2, output) # 最初のデータセットにグループ分けの結果を付ける
for (i2 in 1:kNumber) { #
Data101 <- subset(Data3, Data3$output == i2)# outputが1のサンプルのデータを別に作る
Data101$output <- NULL # outputの列を消す
n1 <- nrow(Data101) # outputが1のサンプルのサンプル数を計算
Ave1 <- colMeans(Data101) # outputが1のサンプルの各変数の平均値を計算
Var1 <- var(Data101)*(n1 - 1)/n1 # outputが1のサンプルの共分散行列を計算
MD <- mahalanobis(Data1, Ave1, Var1)/k # MD（の２乗）を計算
Data4 <- cbind(Data4,MD)
colnames(Data4)[i2+1]<-i2
} #
Data5 <- Data4
Data4$YData <- NULL # Yの列を消す
MinMD<- apply(Data4, 1, min)
MinMD<- as.data.frame(MinMD)
Data5 <- cbind(Data5,MinMD)
Data5$YData <- factor(Data5$YData)# Yの列を文字型にする
ggplot(Data5, aes(x=YData, y=MinMD)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描く
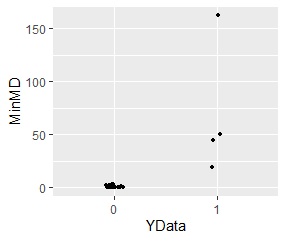
２つのグループのどちらからも離れたサンプルは、MDが高くなっています。
同志社大学 金明哲先生のページ
Rと判別分析
https://www1.doshisha.ac.jp/~mjin/R/Chap_18/18.html
マハラノビス距離を使う判別分析として、混合分布MT法とほぼ同じ方法が紹介されています。
このページのコードを作る時に参考にさせていただきました。
