Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
1つの変数だけで決まっている異常は、その変数をグラフにすれば簡単に分析できます。 「5以上は異常」といったデータの見方ができます。
ところが、2つ以上の変数で決まっている以上は、データを見ているだけでは、 「5以上は異常」といったシンプルなデータの見方ができません。 このページの方法は、多変量でも異常度をシンプルに表現する方法になります。
このページのコードは、入力データに「Y」という名前の変数が入っていることを想定しています。
「Y」の変数は、「0」と「1」の2つの数値が入っていることを想定しています。 「0」のサンプルは、単位空間であることを想定しています。 「0」のサンプルだけでモデルが作られます。
「1」のサンプルは信号空間です。 単位空間のデータに対して、異常なのかを見たいデータになります。
Y以外の変数は、名前に決まりはありません。
計算結果はグラフになるようにしましたが、定量的な結果として、誤判別になるサンプル数がわかるようにもしてみました。 最後に出てくる数値がそれです。
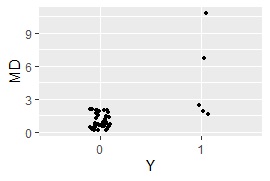
基本的な MT法 の場合です。 この場合は、量的変数しか使えません。 質的変数が含まれる場合は、下に差し替えの方法を書きました。
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data# 質的変数がある場合にこの行を差し替え
Data2 <- subset(Data1, Data1$Y == 0)# Yが0のサンプルのデータを別に作る
Data2$Y <- NULL # Yの列を消す
n <- nrow(Data2) # Yが0のサンプルのサンプル数を計算
Ave1 <- colMeans(Data2) # Yが0のサンプルの各変数の平均値を計算
Var1 <- var(Data2)*(n-1)/n # Yが0のサンプルの共分散行列を計算
k <- ncol(Data2) # 変数の数を計算
Data1$Y <- NULL # Yの列を消す
MD <- mahalanobis(Data1, Ave1, Var1)/k # MD(の2乗)を計算
Data3 <- cbind(Data, MD)# 元のデータとマハラノビス距離の計算結果を合わせる
Data3$Y <- factor(Data3$Y)# Yの列を文字型にする
ggplot(Data3, aes(x=Y, y=MD)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描く
MaxMDinUnit <- max(subset(Data3, Data3$Y == 0)$MD)# Yが0のサンプルのMDのMaxを求める
Data6 <- subset(Data3, Data3$Y == 1)# Yが1のサンプルを抜き出す
nrow(subset(Data6, Data6$MD < MaxMDinUnit))# Yが1で、Yが0のサンプルのMDのMaxよりも小さなサンプル数を求める
MT法のコードは、量的変数のみにしていますが、質的変数が含まれる場合は、
「Data1 <- Data# 質的変数がある場合にこの行を差し替え」
となっている1行を、下記の2行に書き変えます。
library(fastDummies) # ライブラリを読み込み
Data1 <- dummy_cols(Data,remove_first_dummy = TRUE,remove_selected_columns = TRUE)# 質的変数はダミー変換
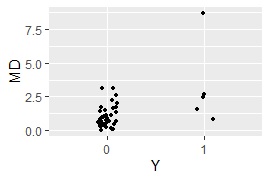
主成分MT法 の場合です。 質的変数が混ざっていてもできるようにしてあります。
基本のMT法では、多重共線性で計算ができない場合に役立ちます。 「変数の数 > サンプルの数」でも役立つ場合もあります。
library(dummies) # ライブラリを読み込み
library(ggplot2) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 加工用のデータを作る
Y <- Data1$Y# Yのデータを別に作る
Data1 <- dummy.data.frame(Data)# 質的変数はダミー変換
Data1$Y <- NULL # Yの列を消す
Data2 <- subset(Data1, Data$Y == 0)# Yが0のサンプルのデータを別に作る
Data2$Y <- NULL # Yの列を消す
model <- prcomp(Data2, scale=TRUE, tol=0.01)# Yが0のサンプルのデータで主成分分析のモデルを作る。
寄与率の小さな主成分は除く
Data3 <- predict(model, Data1)# 主成分得点を取る
Data4 <- subset(Data3, Data$Y == 0)# 単位空間のデータを別に作る
n <- nrow(Data4) # Yが0のサンプルのサンプル数を計算
Ave1 <- colMeans(Data4) # Yが0のサンプルの各変数の平均値を計算
Var1 <- var(Data4)*(n-1)/n # Yが0のサンプルの共分散行列を計算
k <- ncol(Data4) # 変数の数を計算
MD <- mahalanobis(Data3, Ave1, Var1)/k # MDの2乗を計算
Data5 <- cbind(Data, MD,Data3)# 元のデータ、マハラノビス距離、主成分得点を合わせる
Data5$Y <- factor(Data5$Y)# Yの列を文字型にする
ggplot(Data5, aes(x=Y, y=MD)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描くく
MaxMDinUnit <- max(subset(Data5, Data5$Y == 0)$MD)# Yが0のサンプルのMDのMaxを求める
Data6 <- subset(Data5, Data5$Y == 1)# Yが1のサンプルを抜き出す
nrow(subset(Data6, Data6$MD < MaxMDinUnit))# Yが1で、Yが0のサンプルのMDのMaxよりも小さなサンプル数を求める
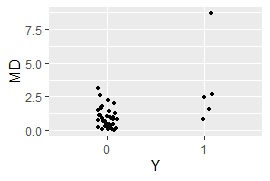
カーネル主成分MT法 の場合です。 質的変数が混ざっていてもできるようにしてあります。
library(dummies) # ライブラリを読み込み
library(ggplot2) # ライブラリを読み込み
library(kernlab)# ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data # 加工用のデータを作る
Y <- Data1$Y# Yのデータを別に作る
Data1 <- dummy.data.frame(Data)# 質的変数はダミー変換
Data1$Y <- NULL # Yの列を消す
Data2 <- subset(Data1, Data$Y == 0)# Yが0のサンプルのデータを別に作る
Data2$Y <- NULL # Yの列を消す
model <- kpca(as.matrix(Data2),kernel="rbfdot",kpar=list(sigma=0.1))# Yが0のサンプルのデータでカーネル主成分分析のモデルを作る
Data3 <- predict(model, as.matrix(Data1))# 主成分得点を取る
Data4 <- subset(Data3, Data$Y == 0)# Yが0のサンプルのデータを別に作る
n <- nrow(Data4) # Yが0のサンプルのサンプル数を計算
Ave1 <- colMeans(Data4) # Yが0のサンプルの各変数の平均値を計算
Var1 <- var(Data4)*(n-1)/n # Yが0のサンプルの共分散行列を計算
k <- ncol(Data4) # 変数の数を計算
MD <- mahalanobis(Data3, Ave1, Var1)/k # MDの2乗を計算
Data5 <- cbind(Data, MD,Data3)# 元のデータ、マハラノビス距離、主成分得点を合わせる
Data5$Y <- factor(Data5$Y)# Yの列を文字型にする
ggplot(Data5, aes(x=Y, y=MD)) + geom_jitter(size=1, position=position_jitter(0.1))# 一次元ジター散布図を描く
MaxMDinUnit <- max(subset(Data5, Data5$Y == 0)$MD)# Yが0のサンプルのMDのMaxを求める
Data6 <- subset(Data5, Data5$Y == 1)# Yが1のサンプルを抜き出す
nrow(subset(Data6, Data6$MD < MaxMDinUnit))# Yが1で、Yが0のサンプルのMDのMaxよりも小さなサンプル数を求める