多変量解析 で使われるデータには、 一見すると、たくさん変数があっても、様子の似ている組合せが入っている事があります。 主成分分析（Principal Component Analysis：PCA）は、似ている変数でまとめると、数種類になってしまう時に役に立つ方法です。
主成分分析では、たくさんの変数を、特徴の順にまとめ、新しい変数を作ります。
主成分分析の「主成分」とは、このまとめられた変数の事です。
主成分は、データの特徴を表す尺度になります。
質的データ の場合に主成分分析に近い方法として、 コレスポンデンス分析 と 数量化Ⅲ類 があります。
主成分分析は、使い道がいろいろあります。 そのため、このサイトでも、いろいろなところで登場します。
上記で紹介した使い道です。 他の多変量解析で、データの前処理に使う方法です。
主成分を、前処理された変数として使う使い方です。
実務で 多変量解析 をする時は、 多重共線性 があったり、「変数の数 ＞ サンプルの数」になっていて、困ることがありますが、 こういった状況でも、とりあえずデータ解析を進めたい時の対策として使えます。 （ 中間層を使った解析 ）
主成分分析と組み合わせる手法は、いろいろ考えられます。 このサイトでは、 重回帰分析 と合体させた 主成分回帰分析 や、 MT法 と合体させた 主成分MT法 のページがあります。
主成分分析は、 変数の類似度の分析 の代表的なものです。 多変量データの相関分析 よりは、変数のグループ分けをしやすいです。
ただし、変数のグループ分けを目的とするなら、 独立成分分析 などの方が良いことがあります。 そのあたりの話は、 分解分析の違い のページにあります。
主成分分析は、 サンプルの類似度の分析 でも、 高次元を２次元に圧縮して可視化 の一種になります。 たくさんの変数があって、サンプルの分類が難しくても、変数が１、２個になるまで要約されていると、 散布図を見るだけで、仲間分けができるようになります。
高次元を２次元に圧縮して可視化 の方法の中には、類似度はわかるけれども、「このグループの特徴は何か？」という事を調べられない方法もあります。 主成分分析を使うと、主成分で考察する事ができるので、特徴を考えやすいです。
ただし、主成分分析だけでサンプルの類似度の分析ができるのは、２個までの主成分で、累積寄与率の大部分を占めている場合です。
主成分（主成分得点）を総合評価の点数のようにして使います。 比較的古い主成分分析の解説では、この使い道を紹介しているものが多いようです。
なお、この方法は、１、２個の主成分だけで累積寄与率のほとんどを占めている場合に使える方法です。 比較的古い時期のデータ分析では、変数がそれほど多くないため、 「１、２個の主成分だけで累積寄与率の大部分を占めている」というケースがあった事も、この使い道が紹介される背景にあったようです。
主成分とは、元の変数に係数をかけて、それらを足し合わせて作られた、合成変数のことです。
例えば、X1という変数があり、PC1、PC2、PC3という主成分が求まった場合、
X1 = a1 * PC1 + a2 * PC2 + a3 * PC3
という関係があります。
主成分同士は、無相関なのが特徴です。
因子負荷量というのは、 元のそれぞれの変数と、それぞれの主成分の相関係数です。
主成分同士は無相関なので、因子負荷量を２乗した値は、 寄与率 として使えます。
以下のページがあります。
Rによる主成分分析の基礎
Rによる変数の類似度の主成分分析
Rによるサンプルの類似度の主成分分析
Rによる質的変数の主成分分析
Rによるクロス集計表の主成分分析
R-EDA1
では、様々なところに「PCA」という名前で入っています。
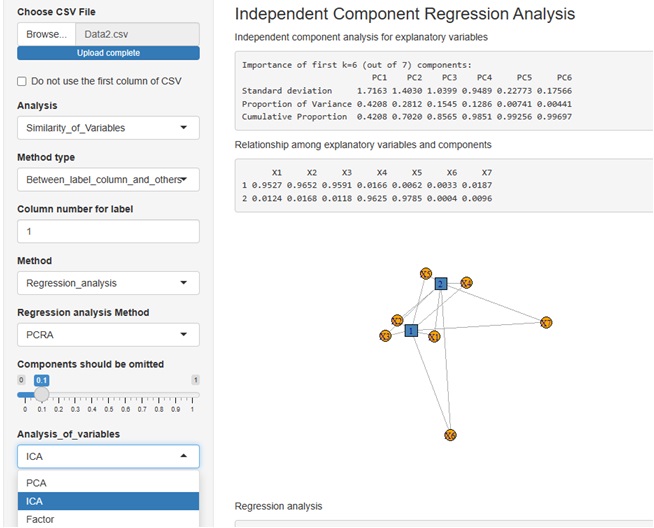
下は、主成分回帰分析の例です。
ICA（独立成分分析）や、Factor（因子分析）と同列で、PCAが入っています。
「図解でわかる多変量解析」 涌井良幸・涌井貞美 著 日本実業出版社 2001
主成分は、合成変数の分散を最大にするものであることや、それを求めるための数学的な手続きが、丁寧に解説されています。
「グラフィカルモデリング」 宮川雅巳 著 朝倉書店 1997
「主成分分析は、
相関係数
を「距離」とする、
多次元尺度構成法
の一種。相関行列を図にして、視覚的に解析できるようにする。」、として、主成分分析の価値を説明しています。
「多変量解析法入門」 永田靖・棟近雅彦 共著 サイエンス社 2001
因子分析の結果の多くは、主成分分析の結果と一致するそうです。
「統計思考入門」 水越孝 著 プレジデント社 2014
この本は、統計的に、また、数字を使って物事を見るための入門書です。
統計学そのものだけではなく、統計学でわかる事や、実際の考えの進め方が中心です。
大きくとらえる --> 違いを見る --> 同じ仲間の中を見る、と言った感じです。
この本の例では、渋谷の109を分析するのに、ファッション業界の中での109の位置を確認し、それから109の中を見ています。
この分析で主に使うのが主成分分析で、
クラスター分析
も使います。
また、分析手法では、判断に迷う時に簡単に白黒つける方法として
判別分析
、予測の方法として、
回帰分析
が登場します。
また、データにはどのような偏りがあるかや、
CVM
と言った、データの取り方の話も重視されています。
「Python機械学習クックブック」 Chris Albon 著 オライリー・ジャパン 2018
7割がデータの扱い方の話、残りが機械学習モデルの話。
特徴量削減で、非線形な時はカーネル主成分分析。
負値がないと時は、。
非負行列因子分解（NMF）
疎データの時は、TSVD（Truncated Sigular Value Decomposition：打ち切り特異値分解）。
「Pythonデータサイエンスハンドブック Jupyter、NumPy、pandas、Matplotlib、scikit-learnを使ったデータ分析、機械学習」 Jake VanderPlas 著 オライリー・ジャパン 2018
NumPy、pandas、Matplotlibで約300ページ。機械学習が180ページ。
主成分分析では、次元削減がうまくできないときの方法として、多様体学習を紹介。
多様体学習の方法は、多次元尺度構成法（MDS）、局所線形埋め込み（Locally Linear Embedding：LLE）、等尺性マッピング（Isometric mapping：Isomap）。
この章のサンプルデータは、「Hello」という文字に見えるように点描された2次元データになっている。
Helloという文字をPNGファイルで保存し、そのPNGからランダムに点を抽出して作っている。
順路
次は
主成分の決まり方
