説明変数だけで 主成分分析 をして、主成分を抽出し、 その主成分を説明変数にして 重回帰分析 をするのが主成分回帰分析です。
「それだけ」と言えば、そうなのですが、この２つの手法の組合せは、強力です。
一般的な重回帰分析では、多重共線性 があるとできません。 主成分同士は、無相関なので、この問題がまったく起きない分析ができるようになります。
一般的な重回帰分析では、「変数の数 ＞ サンプルの数」の時は計算できません。 過学習 を避ける目的では、むしろ、できるだけ「変数の数 ＜ サンプルの数」になるようにします。
主成分分析を重回帰分析の前処理にすることで、「変数の数 ＞ サンプルの数」になっていても、分析を進められることがあります。
※ 主成分では、元の説明変数をあまり要約できない場合、具体的には、主成分をたくさん作らないと、累積寄与率が高くならない場合は、サンプル不足の対策にならないです。
変数が違う時の、わずかな精度の違いは、そのデータだとそうなるというだけで、 長い目で見た時に、一番精度が高くなる変数は、よく考えた方が良いこともあります。
このような時にも、主成分回帰分析で変数のグループを見ておくアプローチは役に立ちます。
主成分回帰分析は、因果関係の分析で、とても役に立ちます。 詳しくは、 主成分回帰分析による因果推論 のページがあります。
Rの実施例が、 Rによる主成分回帰分析 のページにあります。
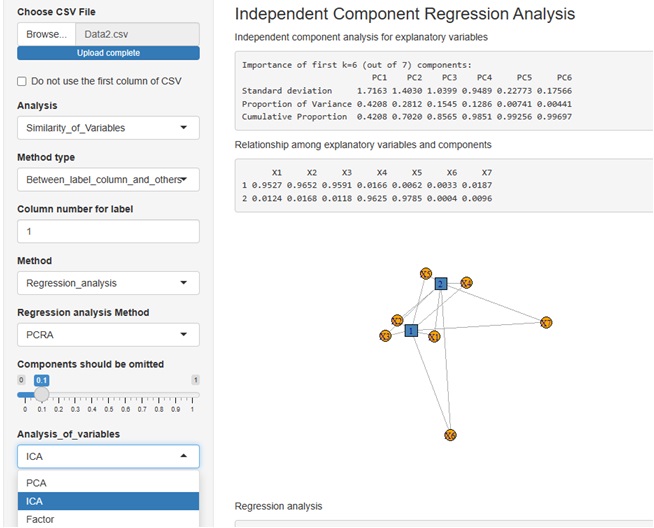
R-EDA1 でもできます。
主成分回帰分析、独立成分回帰分析、因子回帰分析を選べます。
また、説明変数についての主成分分析、説明変数と主成分の関係、モデル説明性、モデルへの主成分の関係について、それぞれ寄与率の分析ができるようにしています。
順路
次は
部分的最小二乗回帰分析
