過学習

過学習は、「過剰に学習している」という意味です。「オーバーフィッティング」とも呼ばれています。データにぴったり合わせるために、モデルを複雑にする事が裏目に出ています。

例えば、たくさんの項を入れた長い式のモデルを作ると、こういった事がおきます。

交差検証法

過学習しているかもしれないモデルを使うのは危険なので、モデルの検証方法が考えられています。交差検証法と言います。

データを２つに分け、片方でモデルを作って、残りを作ったモデルに入力して、予測の精度を検証する方法が簡単です。

ちなみに、この方法は、寄与率やAICによるモデルの妥当性の検証とは異なります。寄与率やAICは、モデルを作成する時に使ったデータに対しての、モデルの妥当性の評価に使われます。

説明変数を増やして、複雑なモデルを作ると、決定係数が大きくなります。増やせば増やすほど、大きくなるのですが、「大きいほど良い」という訳ではないことが知られています。

この現象による、統計学が生む逆説は２種類あります。

まず、目的変数に対して、まったく無関係と考えられる説明変数を増やした時でも起きます。これを知らないと、「決定係数が上がったから、この変数は何か関係しているはずだ」という間違いにつながります。

例えば、下の例では、X1とYは無関係で、X2とYに強い相関があります。このような場合でも、X1とX2を説明変数にして、重回帰分析をすると、X2とYだけの時よりも、わずかに相関係数の絶対値が大きくなります。
過学習

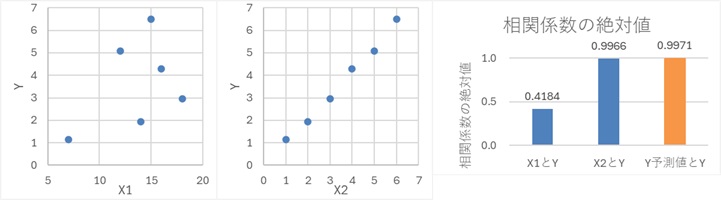
また、学習データ対しての精度は上がったのに、未知のデータについての予測精度は下がることが起きます。これを知らないと、出たらめな予測で、混乱することにつながります。

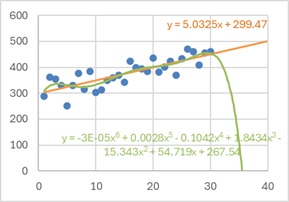
例えば、下の例では、同じデータに対して、説明変数が１個の場合（１次間数）と、６個の場合（６次関数）です。６次関数の方が、データに対してはよく合っているように見えますが、予測をすると、おかしな方向に予測しています。
過学習

順路次は外挿