setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
pairs.panels(Data) # グラフにする
主成分回帰分析 の使い方の紹介になります。
一部を変更すれば、 独立成分回帰分析と因子回帰分析 や、 部分的最小二乗回帰分析（PLS） もできます。
CドライブのRtestというフォルダに、Data.csvというファイルがある状況を想定しています。 目的変数は「Y」という名前になっている必要があります。 Y以外のすべての変数を主成分分析するようになっていますので、説明変数の名前はなんでも良いです。
library(psych) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
pairs.panels(Data) # グラフにする
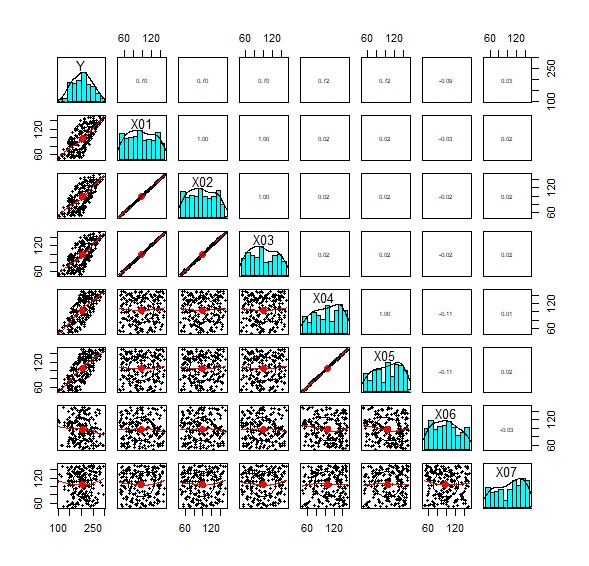
X1、X2、X3は、Yと相関があり、また、X1、X2、X3間も相関があることがわかります。
X4とX4は、相関があることがわかります。 これらのYとの相関は、何となくありそうにも見えますが、よくわからない感じです。
X6とX7は、どれとも相関がないらしいことがわかります。
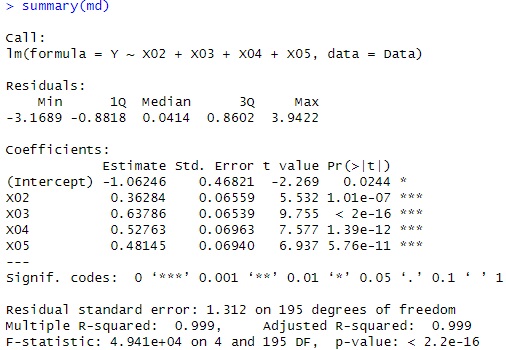
md<-step(lm(Y~.,data=Data))# 重回帰分析（step関数で変数の選択）
summary(md) # 結果
ここからが 主成分回帰分析 です。
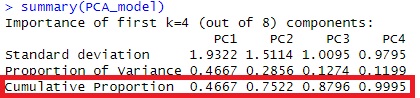
何個の成分までを使うのかを、主成分分析で検討します。 tolの値が小さくすると、累積寄与率への寄与が小さい主成分も含まれるようになります。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T)
DataY <- Data$Y # Yの列を別名で保管する
DataX <- Data
DataX$Y <- NULL # データからYの列を消して、Xの列だけにする
PCA_model <- prcomp(Data, scale=TRUE, tol = 0.1) # Xを主成分分析
MaxN <- ncol(PCA_model$x)# 使う主成分の数
nr <- nrow(Data)# データの行数を求める
nc <- ncol(Data)# データの列数を求める
summary(PCA_model) # 結果
この部分は、手法によって、コードが違います。 出力が、pc1という部分が共通です。
# 主成分分析（PCA）を使う場合
pc1 <- PCA_model$x
# 独立成分分析（ICA）を使う場合
library(fastICA)
ICA_model <- fastICA(DataX, MaxN)# 独立成分分析。抽出成分の数はMaxN
pc1 <- ICA_model$S# 要約変数（独立成分）の抽出
# 因子分析（FA）を使う場合
library(psych)
FA_result <- fa(DataX, nfactors = MaxN, fm = "ml", rotate = "varimax") # 因子分析。潜在変数の数をMaxNと仮定
pc1 <- FA_result$scores
# 部分的最小二乗回帰分析（PLS）を使う場合
library(pls)
PLS_model <- plsr(Y~.,data= Data)# PLS
pc1 <- PLS_model$scores
pc1 <- pc1[1:nr,1:MaxN]
Data4a<-cbind(Data,pc1)
pc2 <- cor(Data4a)^2 # 総当たりで相関係数の２乗を計算
n3 <- nc + 1
n4 <- nc + MaxN
pc3 <-pc2[n3:n4,1:nc]
round(pc3,4) # 少数第4位まで表示
# この結果を見ると、
（PC1,PC2と、X01,X02,X03）、（PC3,PC4と、X06、X07）のグループに分かれています。
Yは、PC1,PC2のグループに依存していることもわかります。
# 主成分と元の変数の相関の強さの全体像を見るためのグラフを作ってみます。
library(igraph)
pc4<-round(pc3,1) # 相関係数の２乗が0.1未満なら、0にする。
pc4<-round(pc4,2)*10 # 相関係数の２乗は最大で1なので、最大の線の太さが10になるようにする
DM.g<-graph_from_incidence_matrix(pc4,weighted=T) # グラフ用のデータを作る
V(DM.g)$color <- c("steel blue", "orange")[V(DM.g)$type+1] # 色を変える
V(DM.g)$shape <- c("square", "circle")[V(DM.g)$type+1] # マークの形を変える
plot(DM.g, edge.width=E(DM.g)$weight) # グラフを作る
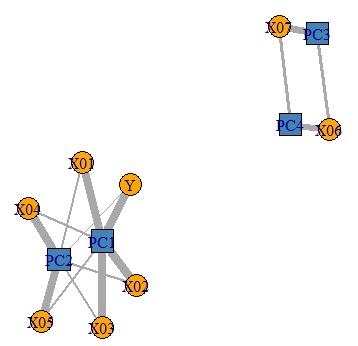
# 表のデータが、グラフで見やすくなりました。
例えば、上記で、独立成分分析をしていれば、以下で使う主成分は、独立成分になります。
DataPCR <- transform(pc1, Y = DataY) # Yと主成分で新しいデータセットを作る
pcr <- lm(Y ~ . ,DataPCR) # 主成分回帰分析
summary(pcr) # 結果を出力
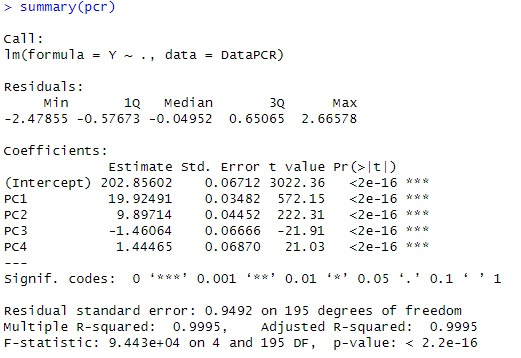
#この例の場合は、PC1とPC2に「***」が付いているので、この２つの変数で決まっているモデルと考えられます。
#主成分同士は無相関なことがわかっているので、step関数はいれていないです。
#このモデルの寄与率は「Multiple R-squared」で、0.9995となっています。
predictedY <-pcr$fitted.values# 予測値
Data3 <- cbind(DataY,predictedY) # 分析用のデータを作る
plot(Data3, cex=0.5)# グラフにする。cexは、プロットの大きさ
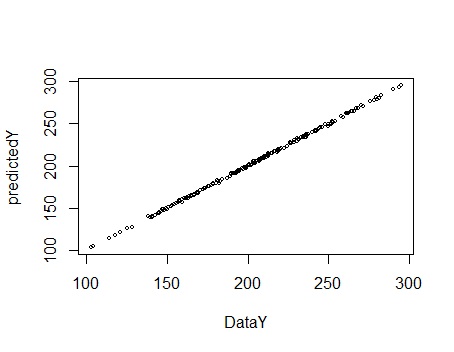
#元データのYと、予測値のYの関係です。
「Multiple R-squared」で、0.9995となったのは、この関係です。
Yに対しての 個別の因子の寄与率 を調べます。 なお、この計算結果と、「元データの変数と、成分の関係の分析」でしている、Yと成分の間の計算結果は同じです。
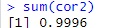
cor2 <- round(cor(DataPCR)^2,4)
cor2 <- cor2[1:ncol(DataPCR)-1,ncol(DataPCR)]# いらない部分を取る
cor2 # 結果を出力
# 成分ごとの寄与率がわかります。
#この寄与率の合計は、上記の「Multiple R-squared」と同じになります。
その検算は下記です。
