主成分回帰分析 では、説明変数を 主成分分析 してから、 重回帰分析 をします。
それと同じ発想で、説明変数について、 独立成分分析 や、 因子分析 をすることもできます。
主成分回帰分析の弱点は、主成分分析をデータの前処理に使っている点にあります。
主成分分析では、主成分を求める時に、データを多次元の分布と見て、分散が最大になる方向を第１主成分、 次に分散が最大になる方向を第２主成分、という風にして主成分が求まって来ます。
このため、 独立成分分析 のページの例にあるように、「因子で分ける」といったことをしたい時に、うまく分けられない方法になっています。
筆者が主成分回帰分析を使いたい時に、 「変数よりも、サンプル数が少ない」や、多重共線性 だけでなく、 説明可能性・解釈可能性 も、よくしたいのですが、「説明可能性・解釈可能性」という点で、主成分回帰分析ではうまく行かないことがあります。
「精度が高いモデルができたけど、物理的な考察ができない」となってしまいます。
部分的最小二乗回帰分析（PLS） という方法があります。 これは主成分回帰分析と似ていて、主成分回帰分析の発展版として知られていますが、説明可能性・解釈可能性という点では、主成分回帰分析よりも良くないです。
分解分析の違い のページで詳しく調べていますが、主成分分析、因子分析、独立成分分析は、一長一短です。
ベストな方法は、データや目的によって違います。 ベストかどうかは、エラーが出るか、といった単純なものではなく、物理的な現象との関係なども含めて考察すると良いです。
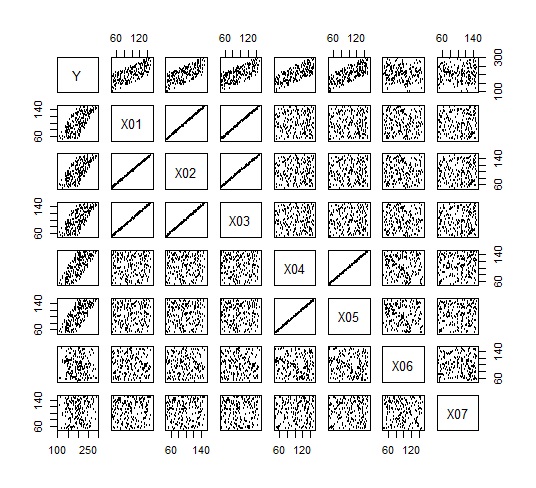
下のようなデータの実施例です。
X01,02,03のグループ、X04,05のグループがあり、グループ内では相関が高いです。
Yは、この２つのグループとは、ある程度相関が見られます。
X06,07は、それぞれ独立しています。
左から順に、独立成分回帰分析、因子回帰分析、主成分回帰分析、部分的最小二乗回帰分析です。
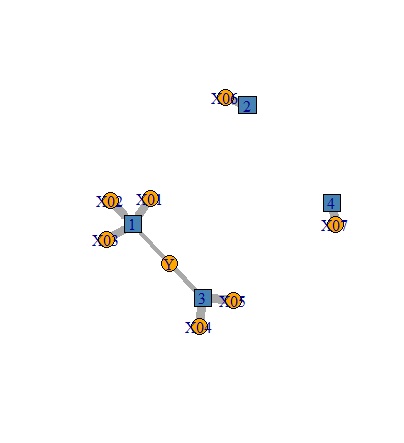
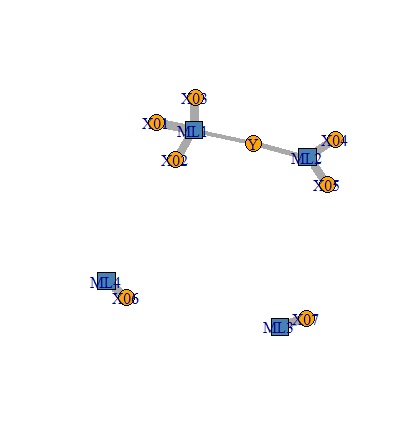
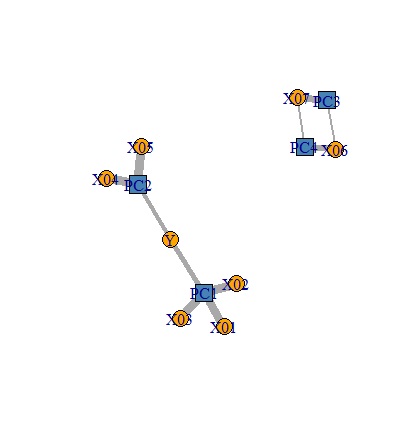
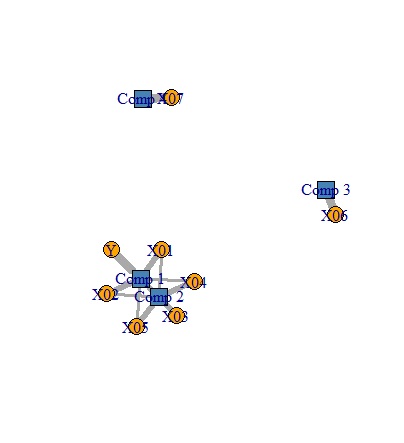
独立成分回帰分析と因子回帰分析の結果は、同じになりました。 まず、Yに対して、２つの成分がつながっています。 さらにその２つの成分は、X01,02,03とX4,5のグループに分かれています。 X06とX07は、それぞれ独立しています。
主成分回帰分析は、独立成分回帰分析や因子回帰分析と似ていますが、X06とX07の独立性が、ひとつの主成分で表せていないです。
部分的最小二乗回帰分析は、X06とX07の独立性は、ひとつの主成分で表せています。 Yは、ひとつの成分とだけ、非常に相関が高いです。X01から05の違いは、主成分の違いには出ていないです。
Rによる主成分回帰分析 のページでは、 主成分分析、独立成分、因子分析、部分的最小二乗回帰分析を使い分けられるようにしています。 上記で、方法の比較をした時のコードも、このページのものです。
R-EDA1 でもできます。
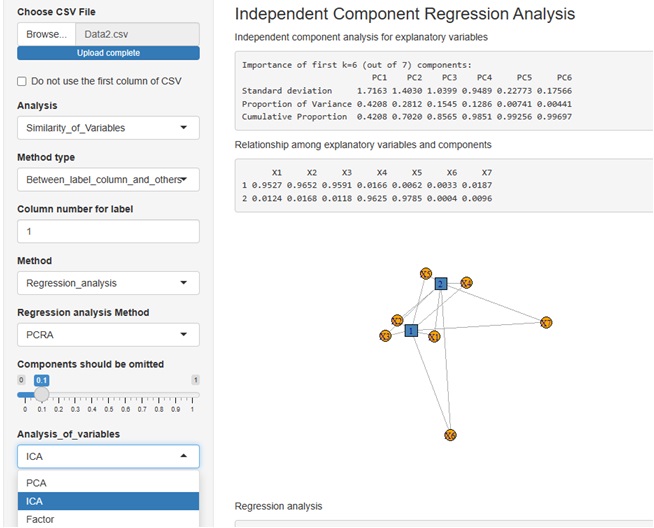
主成分回帰分析、独立成分回帰分析、因子回帰分析を選べます。 下の例は、独立成分回帰分析です。
また、説明変数についての主成分分析、説明変数と主成分の関係、モデル説明性、モデルへの主成分の関係について、それぞれ寄与率の分析ができるようにしています。
順路
次は
独立成分分析のみによる独立成分回帰分析
