このページの内容は、 主成分分析のみによる主成分回帰分析（RAOPCA） と似ています。
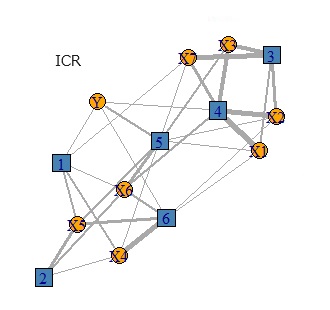
独立成分分析だけで 独立成分回帰分析（ICR） と似た分析をしようとする方法も考えられます。 名前は、RAOICA（Regression Analysis Only Independent Component Analysis）という名前にします。
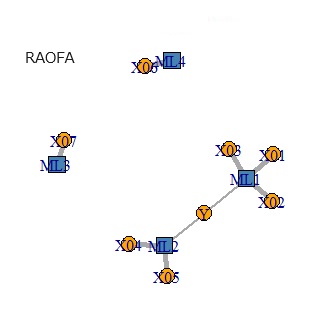
ちなみに、因子分析 だけで 因子回帰分析（FR） と似た分析をしようとする方法も考えられます。 名前は、RAOFA（Regression Analysis Only Factorl Analysis）という名前にします。
目的変数と説明変数を一緒にして、独立成分分析をするところだけが、 RAOPCA との違いです。
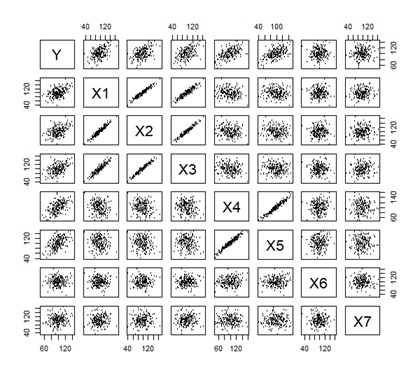
それぞれの変数と、それぞれの独立成分についての組合せについて、相関係数の２乗を計算して分析に使います。
ICR、FR、RAOICA、RAOFAの比較の比較です。 これらの例を見る限りでは、ICRとRAOICAや、FRとRAOFAの組合せは、ほぼ同じでした。
下の図は、左から順に、データ、ICR、FR、RAOICA、RAOFAです。
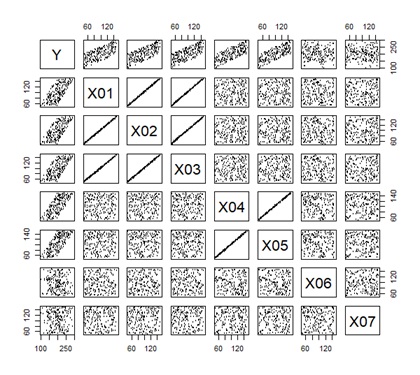
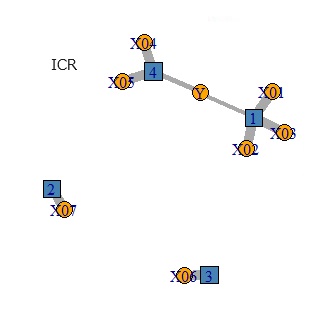
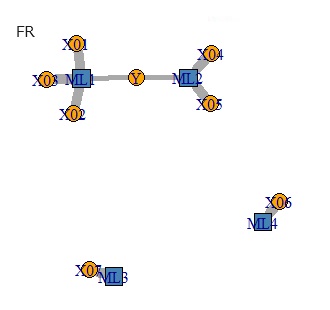
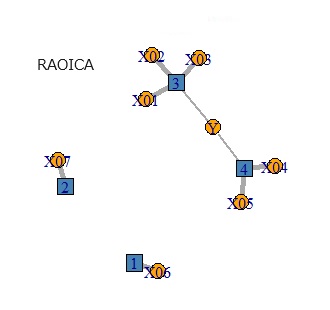
Yからつながる主成分が、２つあるところは、どれも似ています。
下の図は、左から順に、データ、ICR、FR、RAOICA、RAOFAです。
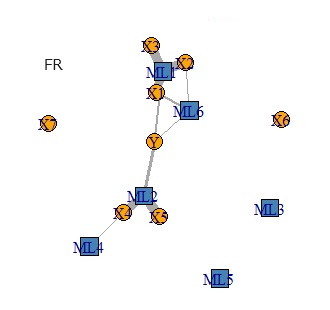
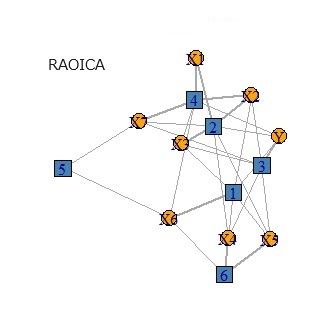
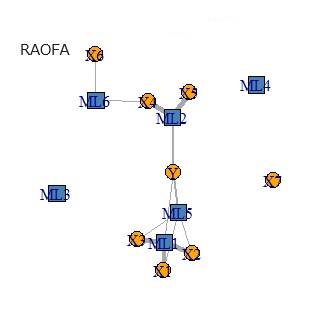
独立成分分析を使っているICARとRAOICAは、成分がうまく分離できていません。
主成分分析のみによる主成分回帰分析（RAOPCA） のページに、「RAOPCAは古くて新しい方法」と説明しました。
RAOICAとRAOFAについても同様ですが、「主成分回帰分析の主成分に、独立成分分析や因子分析を使う」という方法を筆者は見かけたことがないので、 珍しさや新しさの点では、RAOICAとRAOFAは、RAOPCAよりも上です。
順路
次は
変数の選択
