多変量解析 、 データマイニング 、 機械学習 では、目的変数に関係のない説明変数を解析から除いたり、 多重共線性 の関係のある説明変数を整理するために、説明変数を選ぶ作業があります。
（ソフトによっては、説明変数の選択を、自動でやってくれる機能が付いていることもあります。 一方で、変数の選択には配慮がなく、すべての説明変数を回帰式（予測式）に入れることしかできないソフトもあります。）
機械学習 では、「変数の選択」のことを「 特徴量選択 」と呼んでいます。
変数の選択は、３つのポイントがあります。
「変数が１個の場合、２個の場合、３個の場合、、、」と変数の組合せを選ぶ作業ですが、変数の数が増えると膨大になり、 コンピュータで自動で評価するとしても、現実的な時間で終わらない分量になります。
方針は、「最高のモデルではなく、良さそうなモデルを選ぶ」という考え方です。 悪く言えば「妥協する」ですが、良く言えば、「不可能を可能にする」アイディアです。
モデルを作る時に、「あらゆる可能性の中で、一番高い精度のモデルを作りたい」という気持ちになりがちですが、 どんなに工夫したとしても、作られたモデルは、手持ちのデータから作られたモデルです。 未来のデータなど、持っていないデータについては、精度が判断できません。 そのため、「手持ちのデータで作ることができる最高のモデル」でなければならない必要性は、 コンペなどで順位を決める時はありますが、実用面では、あまりありません。
「オッカムの剃刀（かみそり）」と言う名前で紹介されることがありますが、 「変数の数が少ないモデルは良いモデル」という考え方があります。
経験的に、変数の数が少ないモデルは、汎用的なことが多いです。
また、変数の数が少ないモデルを作ってから、選ばれた変数と、選ばれなかった変数の類似点の考察を進めると、 定量的な仮説の探索 が進みます。
一般的にモデルの良さを評価する方法として、 目的変数が量的変数の場合は、 相関係数（決定係数） 質的変数の場合は、正解率や 質的データの相関性 があります。
これらの尺度で高く評価されるモデルは、良いモデルです。
ただ、これらの尺度には、「変数の数が多いほど、評価が良くなる」という性質が含まれているため、これらの尺度だけで判断すると、 過学習 を起こしやすくなります。 また、「変数の数が少ないモデル」が見つかりにくいです。
探索的にモデルを決める方法には、上記の３つのポイントへの対策があります。
変数増加法は、１変数だけで、もっとも良いモデルから始めます。 ２変数の組合せは、最初に選んだ１変数に加える形で、２つ目を選びます。
決定係数に加え、標準偏回帰係数や分散比などの、 変数の重要度 の大きさがわかる尺度を見て、良さそうなモデルを作ります。 また、 トレランスを見たりして、 多重共線性 の関係のある変数は含まないようにします。
変数減少法は、すべての変数を使ったモデルを作って、影響度の低い変数を差し引いていく方法です。
変数増加法と似ているのですが、変数を増加（追加）してから、p値を再計算した時に、有意ではなくなる変数があれば、それは削除します。
変数増加法や、変数減少法は、最小の組合せや、最大の組合せをスタートにして探索する方法です。 これらの方法の弱点として、局所最適に落ち込んでしまう可能性があります。
最小や最大の組合せではないところをスタートにして、探索を始め、 発見的に変数を選択する方法として、 遺伝的アルゴリズム を使う方法もあります。
情報量基準 （AICなど）には、変数を選び過ぎると値が悪くなる性質があるため、決定係数の弱点を補う使い方ができます。
上記の、変数増加法、変数減少法、変数増減法、遺伝的アルゴリズムなどを実施する時の、評価基準として使えます。
ラッソ回帰 は、「変数を選ぶ」という手順ではないのですが、 「不要と考えられる変数は、モデルの係数がゼロになる」という方法になっていて、結果的に、少ない変数でありながら、精度が高めのモデルになります。
変数増減法（ステップワイズ法）とラッソ回帰の実施例です。 Rによる変数の選択 のコードで実施しています。
結論としては、どちらかが良いとは単純には言えず、両方の結果を合わせて、最終的な結果を考えるのが良いようです。
以下の実施例では、
Y = X1 + 0.95 * X2 + 0.9 * X3 + E（誤差）
というようにして作られているデータを使っています。
X1、X2、X3以外は、X1、X2、X3と相関が高いものの、Yには無関係です。
サンプル数は１万個です。
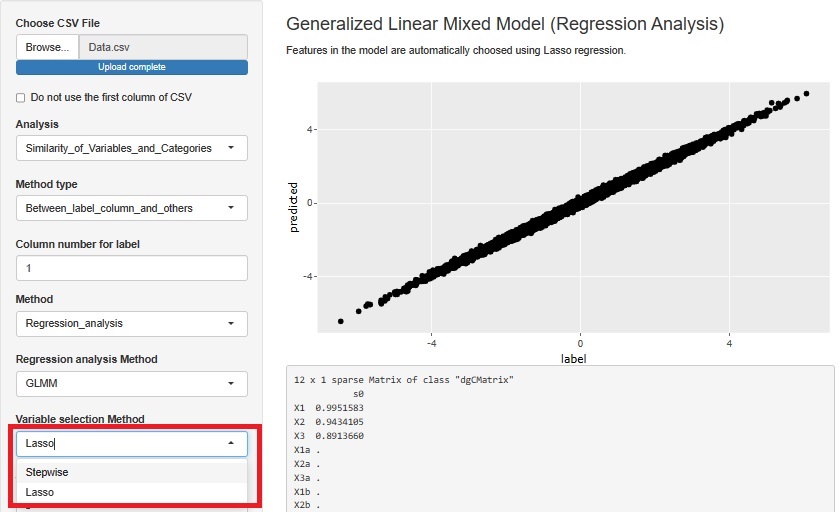
上が、変数増減法の結果で、下がラッソ回帰の結果です。
ラッソ回帰は、変数が完璧に選べています。
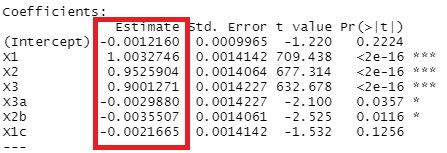
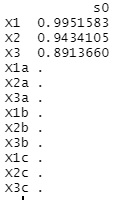
変数増減法の場合に、X3a、X2b、X1cは、入って欲しくないのですが、入っています。 X1、X2、X3に比べればP値が桁違いに大きいので、結論として、「X1、X2、X3で決まっている式」と出しても良いような結果ですが、 「有意」と判断されて入っています。 ステップワイズ法では、p値が判断に含まれるので、サンプル数が少ない時は、シンプルな結果が出やすいです。 サンプル数が多くなると、有意になりやすくなるので、「この変数は含めない」ということが起きにくくなります。
上記の変数に、X1D1、X1D2、X2D1、X2D2、X3D1、X3D2という変数を加えた場合です。 これらは、X1、X2、X3とまったく同じ数値が入っています。 つまり、 多重共線性 があります。
上が、変数増減法の結果で、下がラッソ回帰の結果です。
変数増減法は、多重共線性がない時と、まったく同じ結果になっています。
ラッソ回帰は、多重共線性がある変数について、「３つの内のどれかを選ぶ」ということができていないことがわかります。
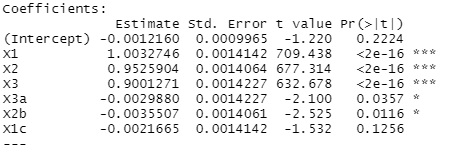
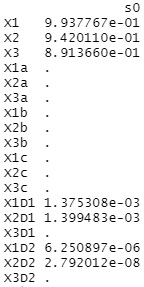
Rによる変数の重要度の分析 のページにある変数増減法では、情報量基準（AIC）を使っています。 このため、まったく同じ数値の変数がある時に、AICが効果的に働いて、「３つの内のどれかを選ぶ」という作業ができています。
ラッソ回帰でもパラメタをうまく設定すれば、「３つの内のどれかを選ぶ」ということができるのかもしれませんが、 その辺りは筆者にはわからないでいます。
Rによる変数の選択 があります。
R-EDA1
では、ステップワイズ法（変数増減法）とラッソ回帰が選べるようになっています。
「情報量規準による統計解析入門」 鈴木義一郎 著 講談社 1995
この本は、確率変数や、
検定
（分散分析）
、
推定
の理論の解説から始まり、一般的な
統計学
の教科書の内容を持っています。
また、
重回帰分析
、
主成分分析
、
自己相関分析
の章もあります。
ここまでなら似た内容の本がたくさんありますが、この本の場合、情報量基準（AIC）の章が真ん中あたりにあり、
分散分析、重回帰分析、自己相関分析
については、「どのモデルが良いのか」という変数の選択を定量的にする方法として情報量基準による方法が入っています。
「情報の物理学」 豊田正 著 講談社 1997
情報量と情報量規準（AIC）の説明の後に、情報量規準を使った変数の選択の話が少しあります。
「オッカムのかみそり 最節約性と統計学の哲学」 エリオット・ソーバー 著 勁草書房 2021
様々な学問の分野では、できるだけシンプルな理論で物事を説明しようとします。
そうした行動に対して「なぜ？」と
哲学
的なアプローチをしています、
順路
次は
スパースモデリング
