相関性と相関係数 のページにあるように、「相関性」と言えば、一般的には、量的変数の類似度の話です。 「相関係数」という尺度は、量的データで計算します。
データの形式は、量的と質的の２種類に大きく分かれますが、 質的変数についても、相関性はあります。
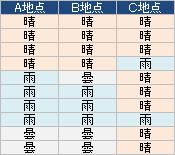
天気のデータの例で言えば、A地点とB地点は、天気が似ているので、「相関が高い」と言えます。 一方、Ａ地点とC地点は、天気が似ていないので、「相関が低い」と言えます。
質的変数の相関性の考え方は、 相関性と相関係数 と似ています。
上記のように、質的変数についても、「相関」と似た考え方はできますが、もちろん、相関係数は計算することはできません。
質的変数について、相関係数と似た特徴のある尺度は、 連関係数 や 相互情報量係数 があります。 両者の比較は、 相互情報量係数 のページにあります。
相関係数には、相関性の検定があります。 質的変数について、相関性の検定と似ているのは、 独立性の検定 です。
質的変数がたくさんある場合、 独立性の検定 、 連関係数 、 相互情報量係数 では、２つずつの変数の組合せについて、すべての組合せを調べることになります。
ひとつの計算で、この分析をする方法として、 対数線形分析 があります。
多変量データの相関分析 では、すべての変数の組合せを見やすく分析する方法として、グラフィカルモデリングを紹介しています。
連関係数 や、 相互情報量係数 は、相関係数と似た性質があるので、これらを使えば、質的変数についても、無向グラフによる分析はできます。
質的変数の有向グラフは、 ベイジアンネットワークによるデータの構造解析 があります。 ちなみに、この方法は、量的変数についてもあります。
ただ、
ベイジアンネットワークによるデータの構造解析
として古くから開発されている方法は、使い勝手が良くないです。
筆者としては、
有向情報量分析
が一番良いと考えています。
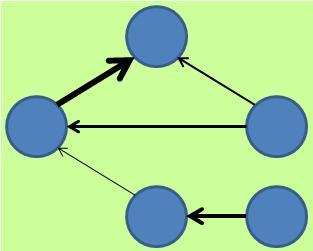
上記では、 多変量データの相関分析 のページで、量的変数用として紹介している方法について、質的変数にも似たものがあることを説明しています。
量的変数、質的変数の両方に似た方法があるのなら、「量的変数用の方法で、質的変数を分析」や、「質的変数用の方法で、量的変数を分析」という応用ができます。
この応用ができると、量的変数と質的変数が混ざっているデータの分析方法にもなってきます。
１次元クラスタリング をすると、量的変数は、質的変数になります。
量的変数を質的変数になると、まず、質的変数の方法で、量的変数と質的変数が混ざっているデータを分析できるようになります。
量的変数を質的変数に変換すると、数値が持っている細かさがなくなるので、粗い分析方法になるのですが、データの特徴をざっくりと把握しやすくなります。 また、 相関性と相関係数 は、２変数の直線的な関係、つまり線形の関係しか扱えませんが、質的変数に変換すると、非線形の関係についての相関性を調べられるようになります。
「質的変数について、変数の類似度の分析をしたい」という時に、「 ダミー変換 して、量的変数用の方法で分析をすれば良い」と思いたくなりますが、ダミー変換では、質的変数の類似度の分析はできません。
ダミー変換すると、カテゴリのひとつひとつが変数になります。 そのため、量的変数用の方法を使うと、 カテゴリの類似度の分析 になってしまい、質的変数の類似度の分析にはなりません。
質的変数を量的変数にすることでも、量的変数と質的変数が混ざっているデータを分析することはできますが、変数の関係の分析ではなく、カテゴリの関係の分析になります。
質的変数にも、相関係数と似た尺度があることを応用して、 主成分分析 について、質的変数用を考えてみたのが、 連関係数を使った主成分分析 です。
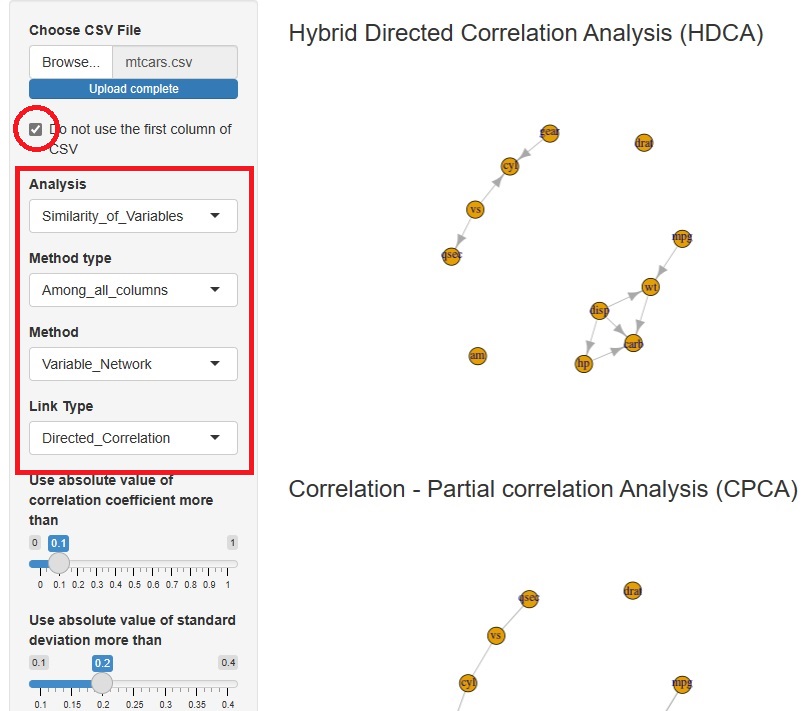
R-EDA1
では、質的変数の無向グラフや有向グラフによる分析が簡単にできるようにしてあります。
これらの機能を使う時は、量的変数は自動的に質的変数に変換してくれます。
順路
次は
分割表
