 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
主成分分析では、相関係数の行列(相関行列)を固有値分析する方法になっています。
「相関係数の代わりに 連関係数 を使ったら、質的変数に対応できるのでは?」というのがこのページのアイディアです。
筆者の思い付きで作った手法です。 先行研究があれば、筆者まで教えていただけると幸いです。
主成分分析で、共分散行列あるいは相関行列を求める部分で、連関係数の行列を求めます。 その後は、主成分分析と同じです。
まず、求めた行列の固有値を求めます。
求めた固有値が、それぞれの主成分の分散を表し、固有ベクトルが、主成分と元の変数の関係を表しているものとみなします。
相関係数は、正負の両方の値があります。 連関係数は、正だけです。 このため、連関係数行列を、相関係数行列の代わりにして、固有値分析をして主成分分析をすることの正当性が、よくわからないでいます。 ただ、以下のように、もっともらしい結果になるので、間違ったことはしていない気はしています。
カーネル主成分分析 では、相関行列を使う計算のところを、カーネル法というものに取り替えることで、様々な表現を可能にします。
相関係数の代わりに連関係数を使うアイディアは、それと似ています。
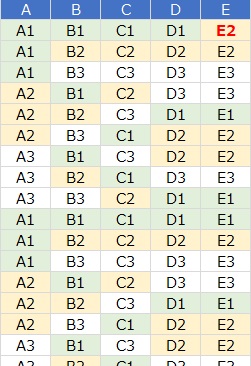
データは、上のようなものです。
サンプル数は、約1000あります。
A、B、C、Dは、3水準系の直交表です。
独立しています。
Eは、1行目が「E2」となっている以外は、並び方が、Dと、まったく同じになっています。
結果は、下になり、きれいにデータの構造がグラフになっています。
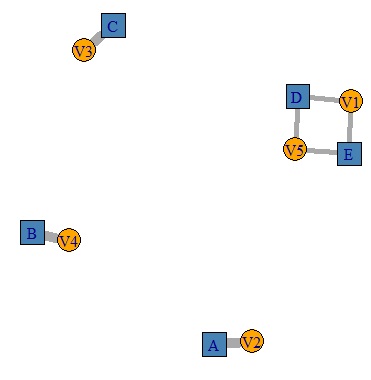
上のグラフは、 Rによる連関係数を使った主成分分析 で作っています。
順路


 次は
偏連関係数
次は
偏連関係数

