主成分分析のルート にあるように、 主成分分析 には複数のルートがあります。 どれを通っても、結果は同じになります。 （正確には、同じになるのは、データを標準化してから、それぞれの処理に進んだ場合です。）
どこかを変形することで、オリジナルの主成分分析（共分散行列・相関行列ルート）ではできなかったことができるようになります。
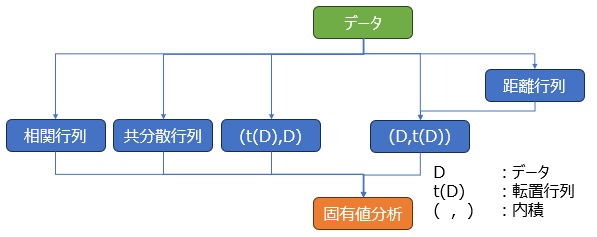
カーネル法 は、内積をしている部分をカーネル関数に置き換えることで、線形の関係を扱う方法を、非線形の関係を扱う方法に変えてしまう方法です。
カーネル主成分分析 と呼ばれる方法がありますが、カーネル主成分分析が置き換える内積は、DtDです。
DtDの時は、内積の行列のサイズがサンプル数と同じになります。 tDDの時は、主成分の数は、最大でも変数の数になるのですが、DtDの場合、関数によっては、主成分の数が、変数の数よりも多くなります。 これによって、「低次元を高次元に変換」ということができるようになっています。
距離行列がユークリッド距離の場合は、普通の主成分分析と結果は同じです。
距離行列を、ユークリッド距離以外のものにすると、普通の主成分分析ではできない分析ができるようになります。
距離は、内積よりもイメージしやすいので、内積を変形させるアプローチよりも、わかりやすいです。
正主成分分析の内積を置き換える方法としては、 コレスポンデンス分析 があります。 頻度データから共分散行列に相当するものを作ります。その後は、固有値問題になるところは、正主成分分析と同じです。 頻度データは、カテゴリの分析に使われるため、一般的な主成分分析とは、違った観点になります。
連関係数を使った主成分分析 が、このサイトにあります。 相関係数の代わりに、 連関係数 を使います。 一般的に、「非線形」というのは、高次元の複雑な曲面をイメージすることが多いですが、 この方法の場合、「質的変数」という種類の非線形を扱えます。
通常の主成分分析では扱えない、非線形への対応としては、データの２乗などの変数を前処理として作ってから、共分散行列・相関行列ルートをするアプローチも考えられます。
このアプローチは、「一般化主成分分析」と呼ばれています。
データの変形以外も含め、上記のアプローチの全部を包括するような主成分分析が、広い意味での「一般化主成分分析」と言えるかもしれません。
「高次元データの次元縮小について」 水田正弘 著 人工知能学会 2007
一般化主成分分析法を紹介している論文です。
一般化主成分分析は、1969年にはすでに文献に出ているそうです。
https://www.jstage.jst.go.jp/article/jsaisigtwo/2007/DMSM-A701/2007_05/_pdf/-char/ja
順路
次は
カーネル主成分分析の種類
Tweet
