カーネル主成分分析 は、カーネル関数の違いで振る舞いがだいぶ変わります。
このページは、その違いを調べてみたものです。
カーネル主成分MT法 では、カーネル主成分分析を説明変数の前処理に使います。 カーネル主成分MT法 の使い道では、カーネル主成分分析は面白い方法です。
このページの下記では、カーネル主成分について、データを要約する能力を見たものです。 詳しくは下記にありますが、非線形のデータを要約する目的では、カーネル主成分分析は役立ちそうもない方法です。
多次元尺度構成法 は、距離を内積に変換してから、固有値分析をします。 そのため、普通の主成分分析と同じ方法になっています。
カーネル主成分分析では、内積をカーネルに変えて、固有値分析をするのですが、 そのカーネルの中に、距離そのものではないものの、距離の関数になっているものを使うことがあります。 ややこしいことになっています。
これらの関数の違いは、 内積の分布とカーネルの分布 のページにあります。
要約分析と分解分析の違い のページがありますが、 主成分分析 には、要約の方法としての期待があります。
カーネル主成分分析には、非線形で普通の主成分分析では、要約できないものを要約してしまう能力に、筆者は興味があるので、調べてみました。 Rによるカーネル主成分分析に、実際に調べた時のコードがあります。
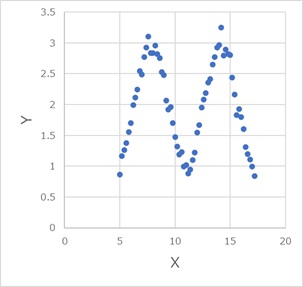
いずれの例も、２変数を１変数に要約できるのかを見ています。
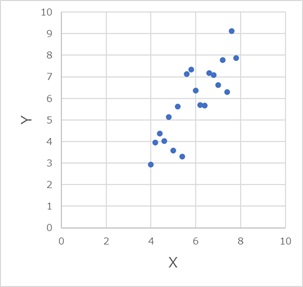
まず、普通の主成分分析が得意な分布です。
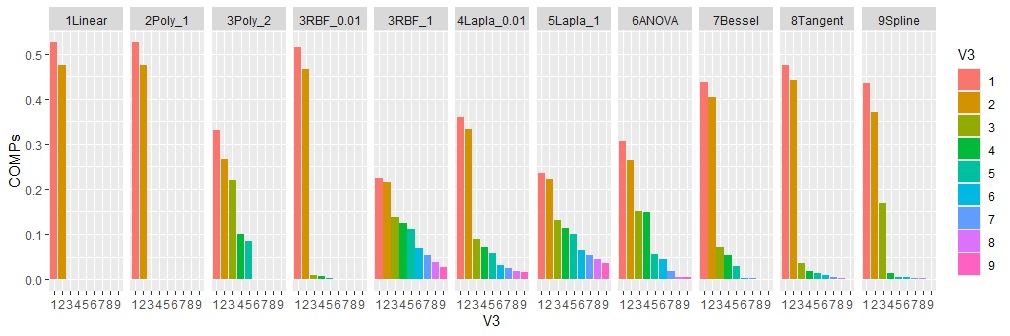
1Linear（vanilladot）は、カーネル関数ですが、線形なので、普通の主成分分析と同じになるものです。予想通りで、普通の主成分分析と同じ結果になりました。
2Poly_1（多項式カーネル）は、１次式なので、1Linearと同じになるはずなのですが、確かに同じになりました。
3RBF_0.01（ガウシアンカーネル）も、1Linearと似ています。 他の例もそうですが、ガウシアンカーネルで係数が小さいと、1Linearとほぼ同じなことがわかりました。
7,8,9もまずまずの結果です。
上記以外は、普通の主成分分析が得意な分布は、不得意なことがわかりました。
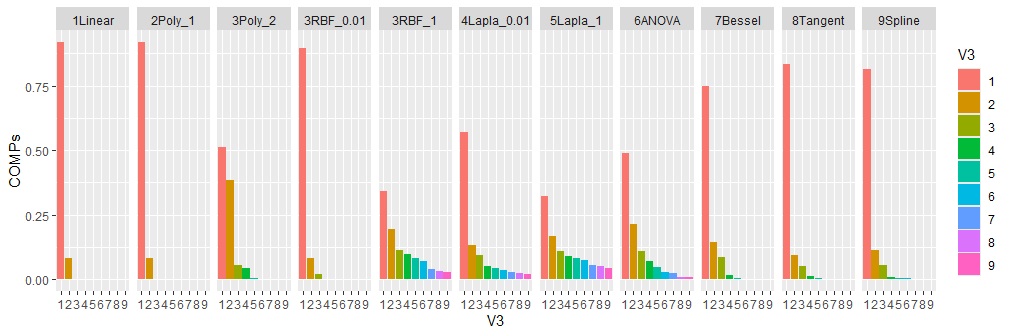
どれも、うまく要約できていません。
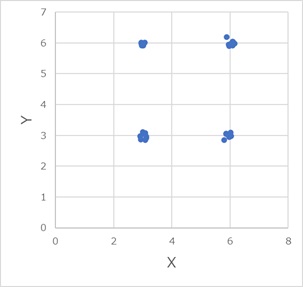
2Poly_1は、二次式のカーネルですが、２乗にするだけでなく、scaleやoffsetも適切な値にしないと、二次式のような分布だとしても、要約できないようです。
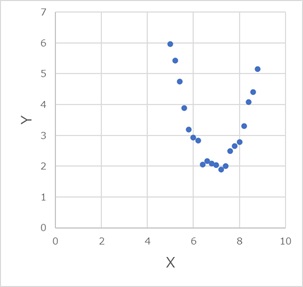
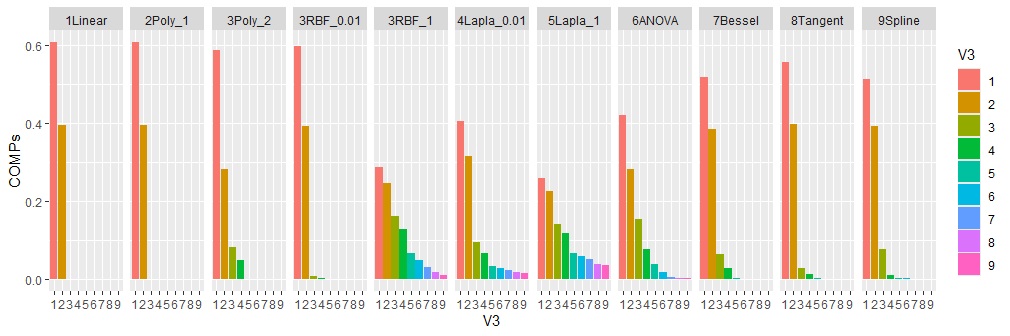
どれも、うまく要約できていません。
どれも、うまく要約できていません。
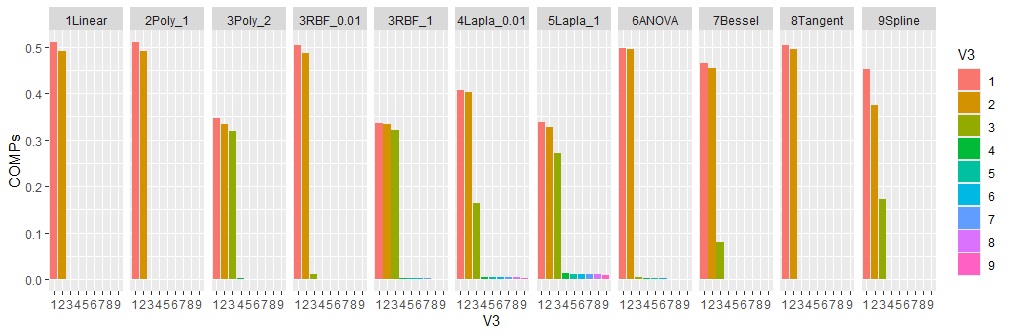
Rによるカーネル主成分分析 があります。
順路
次は
サンプルの関係からの主成分分析
