トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

カーネル法

Data 判別分析やサポートベクターマシンといった方法では、一本の直線（正確には超平面）を引いて、その直線のどちら側に行くのかで、判別しようとします。

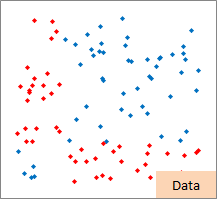
しかし、世の中には、一本の直線で判別しようとする事が難しい場合があり、これが一本の直線で判別する方法の弱点です。右の図の例は、一本という点でも、直線という点でも、判別を表現する事が難しい場合です。

カーネル法は、一本の直線で判別できないデータについても、一本の直線を使う方法で判別しようとするための方法です。

カーネル法のアイディア

右の図の例のように、ある程度明確に分かれているのなら、もともとのデータをうまく変換して、変換したデータに対して、一本の直線で判別できる事があります。カーネル法は、この性質を利用します。

カーネル法は、「低次元のデータを、高次元に写像する事によって、判別しやすくする」と説明される事があります。「次元とは何か？」、と思ってしまいますが、例えば、説明変数が５個あるのでしたら、何らかの加工をする事で５個の変数から、 10個とか、20個の変数を作り出し、その変数を使って、判別できる線を探しています。

具体的には、Xの二乗を計算したものを説明変数にしたり、違うX同士をかけたものを説明変数に加えるイメージです。カーネル法は、中間層を使った解析の一種です。

カーネルトリック

カーネル法を理解するには、中間層を使った解析のイメージがぴったりなのですが、実際のカーネル法では、中間層の部分を計算しません。つまり、Xの二乗を計算したり、違うX同士をかけたものを計算したりしません。

多変量解析の計算の中には、サンプル同士の内積を計算する部分があるのですが、その部分をカーネル関数と呼ばれるものに置き換えて計算しています。

カーネル法を使う解析で実際にするのは、「Xをどうやって変換するのか」ではなく、「カーネル関数を何にするのか」になります。また、カーネル関数を使うと、内積の計算がとても簡単な計算に変わって、計算の量が減ります。これらの特徴は、「カーネルトリック」と呼ばれています。

ニューラルネットワークとの比較

サポートベクターマシンの特徴は、ニューラルネットワークと比較される事が多いです。

ニューラルネットワークは、複雑なモデルでデータを近似するので、当てはまりの良いモデルができるものの、過学習（オーバーフィッティング）の問題があったそうです。また、局所最適になりやすい（良さそうなモデルがいくつかあった時に、一番初めに見つかったモデルで良いと考えてしまう）という問題もあったそうです。

サポートベクターマシンは、これらの問題に陥らない仕組みを持っています。

カーネル法には、「XとYの直接的な関係から調べ始めるのではなく、Xを一度変換し、それとYとの関係を見る」、というアイディアがありますが、これはニューラルネットワークにもあります。

実際にどのような変換がされたのかが、わかりにくい点も同じなのですが、わかりにくさの内容が違っています。ニューラルネットワークの場合は、シグモイド関数や、シグモイド関数の和を使うことによって、変換の部分が複雑になり、実質的にブラックボックスになってしまう事によるわかりにくさです。サポートベクターマシンの場合は、どういう変換がされたのかが、カーネルトリックによって見えなくなっている事によるわかりにくさです。

因果関係の分析の方法として

もともとのデータでは、一本の直線で判別できないものが、カーネル法で判別できるようになるのは、画期的です。

とにかく判別できれば良いのなら、これで良いです。しかし、相関関係の探索として、カーネル法を使った場合は、「なぜ、判別できるのか？」がわかりにくいので、困ったことになります。

カーネルの形からの評価

多項式カーネル（Polynominal）、ベッセル、ANOVA、Tangentは、パラメタが２つ以上あるため、実務で使いこなすのは、難しいようです。

サポートベクターマシンの説明で、「低次元を高次元にするので、判別ができるようになる」という図解をする時に使われるのは、多項式カーネルの事が多いですが、多項式カーネルは扱いが難しいです。

２次曲線のような関係のある２変数は実務でもあるので、多項式カーネルが使いやすいと、良かったのですが、難しいようです。

RBF（ガウシアンカーネル）、ラプラシアン、スプラインは、パラメタが０個か１個なので、実務向きです。 RBFとラプラシアンは、式の中に入っているユークリッド距離が、１乗か２乗かだけの違いなので、振る舞いが似ています。

参考文献

カーネル法は、サポートベクターマシンの本の中で、必ず紹介されています。

「カーネル多変量解析」赤穂昭太郎　著　岩波書店　2008
サポートベクターマシンはカーネル法を使うひとつの方法という書き方をしています。正則化の話も多いです。

「パターン認識と学習の統計学」甘利俊一・麻生英樹・津田宏治・村田昇　著　岩波書店　2003
この本は、パターン認識の手法全般、カーネル法、バギングとブースティングの 3つの部分に分かれていて、それぞれの著者が異なります。
「回転していても文字の意味は変わらない」といった事前知識（メタ知識）を関数として表して使う方法も、カーネル関数の一種として紹介していました。

順路次は内積の分布とカーネルの分布