カーネル法 では、「サンプル同士の内積の計算を、カーネルに取り替えます」という流れがあります。
ところで、サンプル同士の内積の計算は、普段、明示的にすることはなく、内部で自動的にされるものになっています。
そこで、内積の分布はどのようなもので、カーネルにすると、どのように変わるのかを調べてみたのが、このページです。 サンプルの関係からの主成分分析 の疑問から始まっています。
まず、ユークリッド距離は、カイ二乗分布になっています。 内積は、正規分布のような分布になっています。 カーネル関数は、距離や内積の分布から、だいぶ変わっています。 以下の例では、データによる違いのわからないカーネル関数もありました。
今回、２種類用意してみました。 いずれもデータは100行あり、３変数です。 ひとつめは、３つの変数で、非常に相関が高いです。 もうひとつは、非常に相関が低いです。
これ以降も、左側は相関が高いデータ、右側が低いデータの結果です。
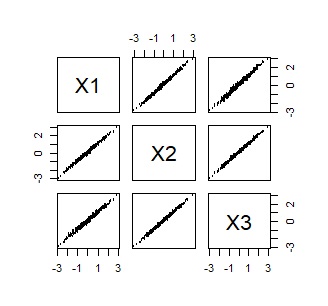
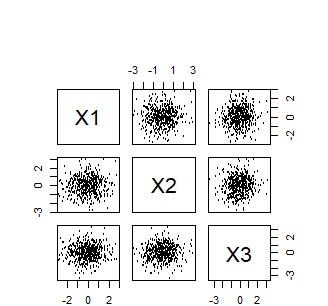
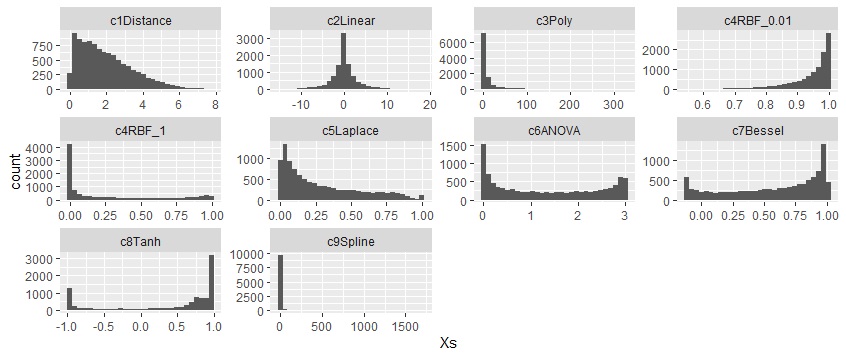
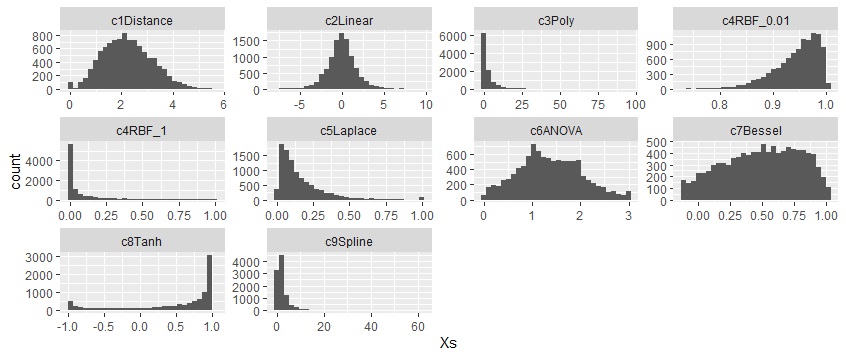
ユークリッド距離 (Distance）、内積（Linear）以外は、カーネル関数です。
距離は、カイ二乗分布になっていてい、相関が低い方が、プラス側に中心があります。
内積は、０を中心とした山型になっていて、相関が高いと、左右の裾野が広くなりつつ、中心も尖っています。
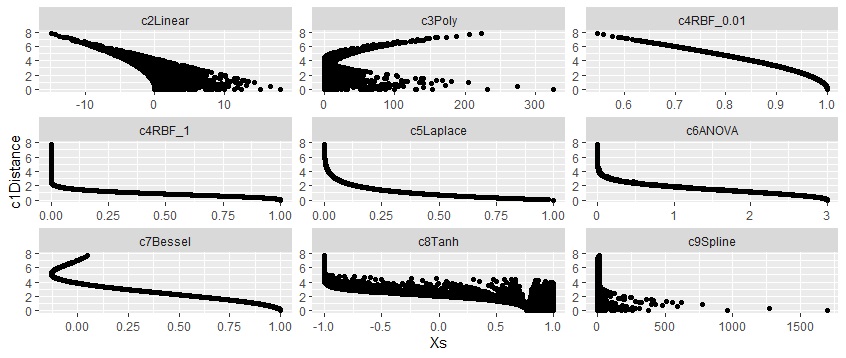
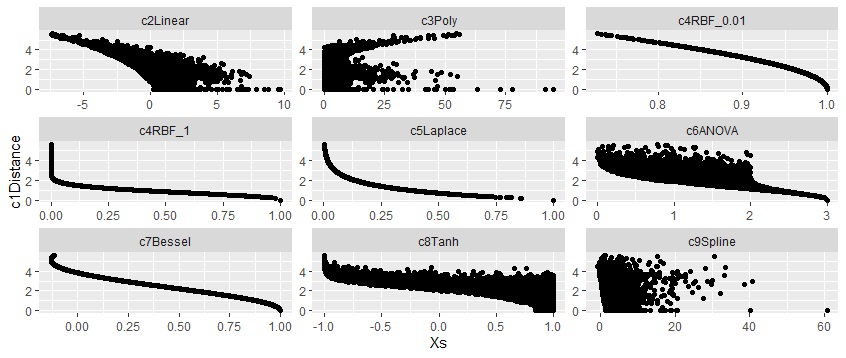
下の図は、Distanceを縦軸にして、その他を横軸にしたものです。
距離が０に近いほど、内積はプラス側に広がっています。 距離が大きいと、内積はマイナス側です。
カーネル関数の中に距離の計算が入っている、RBF、Laplace、Besselは、明確な曲線状になっています。 ANOVAは、相関が高い時は、曲線ですが、低いとばらついています。
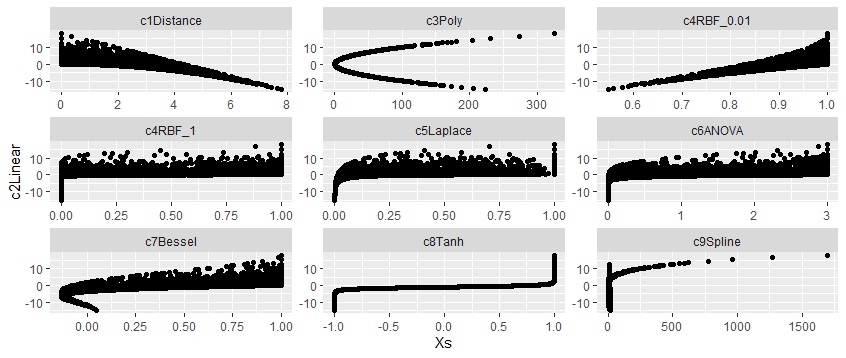
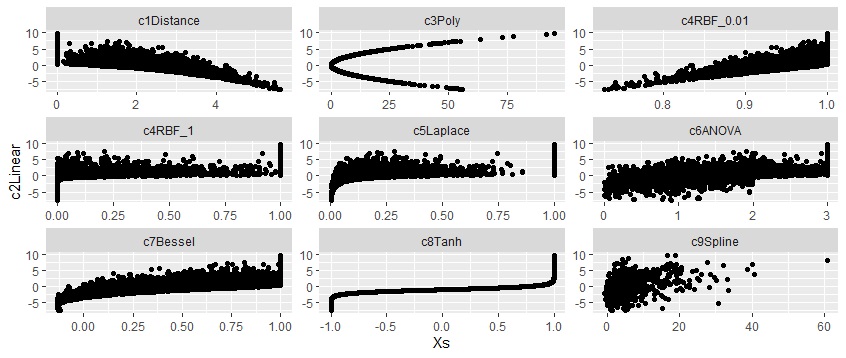
下の図は、Linearを縦軸にしています。
PolyやTanhは、Linearと曲線的な関係になっています。
このページは、 Rによる内積とカーネル のコードで作りました。
順路
次は
One-Class SVM
