共分散の式は、
です。
分散の計算式にデータ数 n で割るもの（標本分散）と、n-1で割るもの（不偏分散）があり、一般的な用途では、n-1 を使う事が多いです。 マハラノビス距離では、nを使います。
ここでは、各サンプルのデータから、その変数全体の平均値を引く処理をいれていますが、 こうすると、全部のデータの重心の位置からの距離になります。 この部分が０なら、原点からの距離になります。 この部分に別のサンプルのデータを入れると、２点間の距離になります。
ユークリッド距離とマハラノビス距離は、かなり似ているのですが、使い道がだいぶ違います。
ここでは、一般的な定義です。 ユークリッド距離との違いが、わかりやすい定義です。 MT法のマハラノビスの距離 は、少し違います。
ここでは、変数が x と y の、2個の場合を例にします。
「 i 」は、「 i 番目のデータ」という意味です。
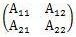
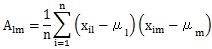
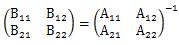
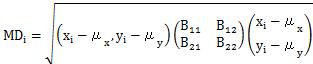
日常生活の中で、「距離」といっている時は、ユークリッド距離のことが多いです。
ユークリッドの距離の求め方は、基本的に直角三角形の斜辺の長さの求め方と同じです。
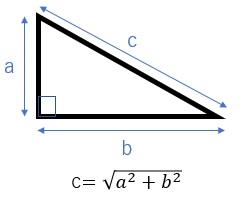
マハラノビス距離の計算方法は、これとはだいぶ違いますが、 「マハラノビス距離とは何か？」を理解するには、ユークリッド距離との比較から始めるのがわかりやすいかと思います。
日常的には、距離というと「A地点とB地点の距離」という言い方をします。 「長さ」と同じ意味で使います。
マハラノビス距離もユークリッド距離も「距離」と付いていますが、「長さ」ではないものにも使えます。 データサイエンス では、「AとBは似ている」ということを表す指標として、距離を使うことがあります。
共分散行列の対角成分が１で、それ以外が０になるデータで計算すると、マハラノビス距離とユークリッド距離が等しくなります。
共分散行列の対角成分が１で、それ以外が０の場合というのは、それぞれの変数の標準偏差が１で、それぞれの変数間に相関がない場合になります。 まったく無関係の項目が変数になっていて、データが 標準化 されていると、この場合に近くなります。
ユークリッド距離は二乗した数の和の平方根で求まりますが、マハラノビス距離は行列の計算や、分散の計算があるので計算が複雑です。
変数間に相関がある時に、マハラノビス距離では、それが計算の中で考慮されます。 ユークリッド距離は、考慮されません。
ユークリッド距離を使う場面では、例えばＸ方向とＹ方向があったりしますが、 日常的な距離の時は、これらは独立しているとみなせるので、相関が考慮されないことで特に問題はありません。
マハラノビス距離では、相関が考慮されるので、変数間に似た性質がある時に、「似た性質」を考慮した指標として使えます。
ユークリッド距離では、元の座標の単位がメートルなら、距離の単位もメートルになります。 距離が単位を持っています。
マハラノビス距離では、どんな単位の変数でも、距離の平均値が「変数の数」になります。
このことからもわかるように、マハラノビス距離は無次元（単位を持たない）になっています。
ユークリッド距離は、具体的な単位があるので、現実の話の中でイメージする使い方ができます。 一方、マハラノビス距離は、そういった使い方ができません。
なお、平均値が一定になる性質と、その利用方法は、 MT法のマハラノビスの距離 で説明しています。
マハラノビス距離では、メートルとキログラムのように、単位の異なる変数が混ざっていても、意味のある指標として使えます。 この利点は、無次元化の良いところです。
一方、単位の異なる変数が混ざったデータに対して、ユークリッド距離を計算するのは、 「メートルの２乗 ＋ キログラムの２乗」のような計算になるため、 次元解析 の観点からは、やってはいけない計算です。
ちなみに、単位を気にせずに、ユークリッド距離を計算すると、数字の絶対値が大きな変数の大きな指標になります。 例えば、キログラムとメートルの２つの変数がある場合と、キログラムの変数をグラムに変換した場合では、ユークリッド距離の計算値は違います。 グラムにした方が、重さの変数の影響がユークリッド距離に大きく現れます。
「計算が簡単」や、「変数間は無相関とみなして問題ない」と考えて、ユークリッド距離を採用する場合は、 標準化や正規化 、 主成分分析 等でデータを前処理してから使うと良いです。 ただし、この使い方では、距離は無次元になりますので、ユークリッド距離を使う利点のひとつが使えません。
順路
次は
多次元の距離の性質
