次元が増えれば増えるほど、距離のばらつきは大きくなります。
「異次元の○○」のような言い方がありますが、次元が増えることによる、ばらつきの増え方は非常に大きいです。
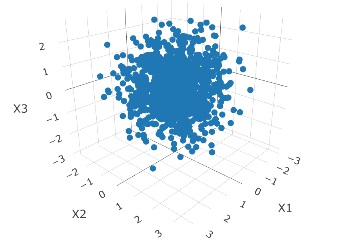
下のグラフは、各変数は、平均値が０、標準偏差が１の正規分布になっているデータです。 ３次元空間上に球状にばらついています。
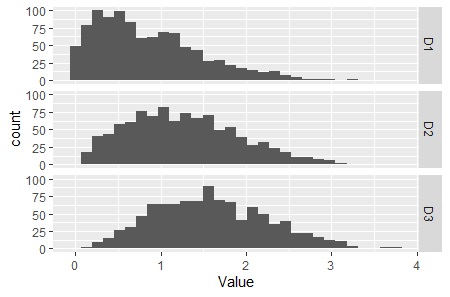
ヒストグラムの方は、１つの変数だけで計算した距離、２つの変数で計算した距離、３つの変数で計算した距離、というようにして、 ユークリッド距離を計算したものです。 平均値が増えると、分布の中心が右にずれていき、全体的な範囲が右に広がっている様子がわかります。
品質工学 では、 MT法 という、マハラノビス距離を使う方法が開発されています。
マハラノビスの距離 のページに詳しく書きましたが、 MT法 では、マハラノビス距離の定義として、変数の数で割る部分があります。
一般的に知られているマハラノビス距離は、距離の平均値が変数の数と同じになる性質があるのですが、 変数の数で割るので、変数の数に関わらず、平均値が１になります。
こうすることで、変数の数を気にせずに、「１より大きいのか？」という視点で分析できるようになっています。
「変数が多いと、多くの情報を考慮した分析ができる」というのが、変数が多いことの利点です。
一方、変数が多いとばらつきが増大するため、判断に必要なサンプル数が増大します。 これが、変数が多い分析の弱点です。
距離の計算では、０よりも小さな数字はありません。 次元が増えると、ばらつきが大きくなるという性質は、プラス側に対して起こる現象で、０より小さな領域には入って行きません。
マイナスの距離が出て来るような世界は、数学的には定義できそうです。 ただ、現実の世界の理解について、少なくとも日常的な場面では、役に立ちそうもないです。。。
順路
次は
多次元の距離の適正化
