標準化と正規化

統計的なデータ分析の方法は、変数の単位は気にせずに、数字の大きさだけが対象になります。このため、あまり意味のない変数なのに、数字が大きな変数だと分析の中で目立って来ることがあります。

標準化も正規化も、異なる単位の変数が混ざったデータの分析で、変数を平等に扱うのに便利な方法です。

標準化

標準化（Standardization）は、元のデータから平均（Average：Ave）を引き、それを標準偏差（Standard Deviation：StDev）で割ります。

標準化

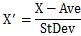
の形です。

この変換を行われたデータ群は、平均が0、標準偏差が1になり、無次元化されています。

このサイトでは「標準化」というページが、経営学の中でも登場しますが、ここの「標準化」とは無関係です。

標準化では、平均を引いてから、標準偏差で割りますが、平均を引くだけの場合は、「中心化」と呼ばれることがあります。

中心化は、変数毎に単位は同じだけれども分布が違う場合に、中心をそろえて、分布の違いをわかりやすくする方法として使えます。

正規化（Normalization）は、元のデータから最小値（Minimum：Min）を引き、それを範囲（レンジ：Range）で割ります。範囲というのは、最大値（Maximamum：Max）と最小値の差です。

標準化

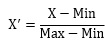
正規化されると、数字が0から1の間になります。 100をかけると、0から100の間になり、こうすると、小数点以下の細かいことを気にしなくて良いので、数字の見通しがよくなることもあります。

正規化をすると、数字が0から1の間になり、範囲が決まっている性質が便利になることがあります。全部の変数を同じ扱いをしたい時や、範囲のどの位置に個々のサンプルがあるのかを知りたい時に使えます。

標準化をすると、範囲が変数ごとに違います。標準化をすると、だいたいのサンプルは、0から1の範囲に入り、外れ値になるほど1よりもずっと大きい数字になるため、外れ値の観点を分析にいれたい時に使えます。