標準化や正規化 をした場合や、 主成分分析 で作る主成分は、データの前処理として使われます。 いずれも、元のデータと値の範囲が変わっています。
データによっては、主成分を作った後で標準化や正規化をすると、データの特徴がさらにわかりやすくなることがあります。 下記は、単独で使う時と、組み合わせて使う時についての例です。 例１が、単独でも効果が十分にあって、組合せの効果がない例です。 例２は、組合せの効果が大きくて、組合せないと、その後の分析が難しい例です。
下記では、 高次元を２次元に圧縮して可視化 の方法のUMAPをする時に、前処理が違うとどうなるのかを見ます。
主成分分析は、相関行列を使う方（スケーリングあり）を使っています。
高次元を２次元に圧縮して可視化
のページの例4-1と同じデータです。
２つの軸で値の範囲が桁違いになっています。
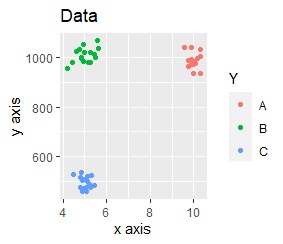
桁違いの影響が大きく出てしまい、グループが２つに分かれ、AとBの区別ができなくなっています。
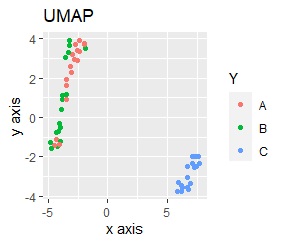
左から標準化（Standardization）のみ、正規化（Normalization）のみ、主成分分析（PCA）のみです。
いずれも、３つのグループがきれいに分かれました。
きれいに分かれる理由は、「桁違い」という特徴がなくなったからです。 標準化、正規化、また、スケーリングありの主成分分析は、変数間に桁違いの特徴がある時に、その特徴を消す効果があることは、 よく言われていることですが、その通りの結果になりました。
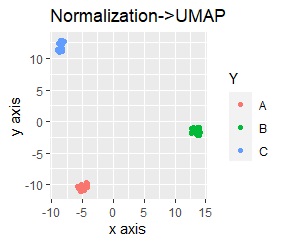
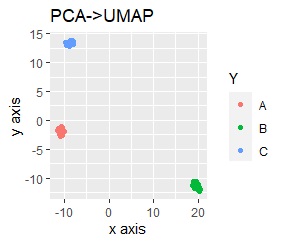
左が主成分分析（PCA）の後に正規化（Normalization）をしています。
単独でも十分に効果が出ているものなので、特に変わらないです。
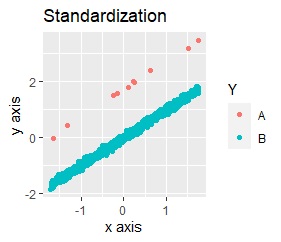
分析対象のデータです。 Bが大多数の分布で、Aが外れ値のようになっています。
二重測定
のデータや、
多重共線性
のある中で
外れ値
がある時に、このようなデータになることがあります。
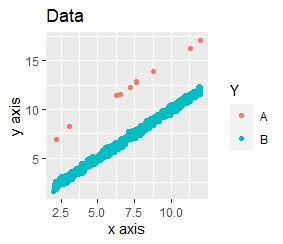
色を付けているので、Aがどこに配置されたのかがわかりますが、色がないと、元のデータの特徴が見えなくなっています。 重なって見にくいのですが、Aは下の方の他に、上の方にも配置されています。
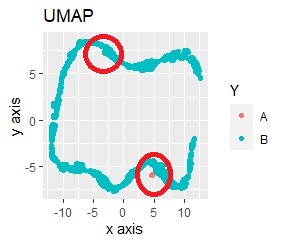
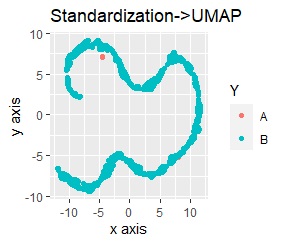
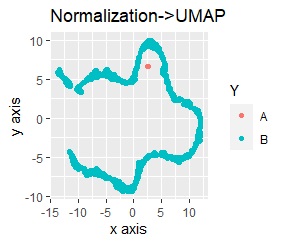
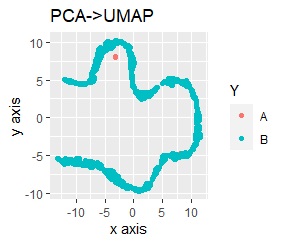
左から標準化（Standardization）のみ、正規化（Normalization）のみ、主成分分析（PCA）のみです。
いずれも、外れ値のAが一つの塊になって、Bから少し離れています。
UMAPをする前の、前処理だけの結果は下図になっています。
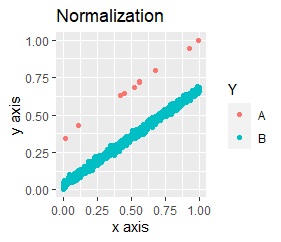
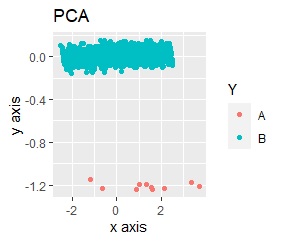
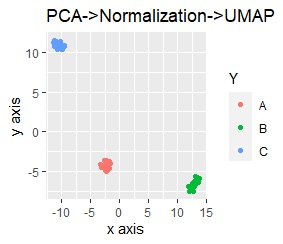
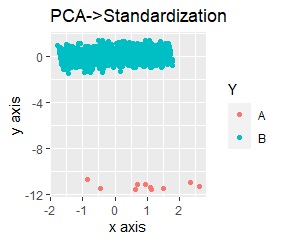
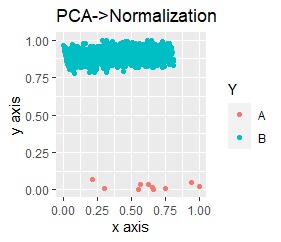
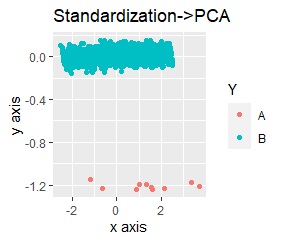
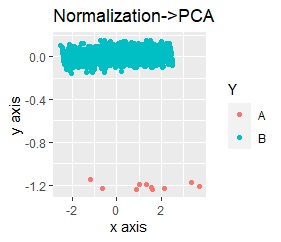
左が主成分分析（PCA）の後に標準化（Standardization）、右が主成分分析（PCA）の後に正規化（Normalization）です。
Aの塊が、完全にBから離れています。 特に標準化の方が、正規化よりも明確に分かれています。
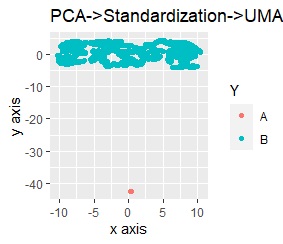
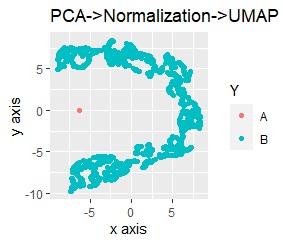
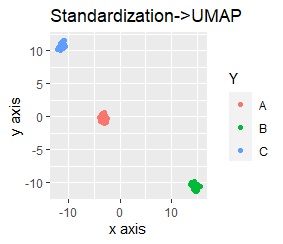
UMAPをする前の、前処理だけの結果は下図になっています。 グラフをパッと見た感じは、PCA単独の時と変わらないですが、それぞれの軸の数字を見ると、値の範囲が変わっています。
PCAだけの時の、「縦軸の範囲／横軸の範囲」は、「1.4／7 ＝ 0.2」です。 PCAと標準化（Standardization）の時は、「14／5 ＝ 2.8」です。 PCAと正規化（Normalization）の時は、「1／1 ＝ 1」です。
この比率は、PCAと標準化、PCAと正規化、PCAだけの順番です。 そして、この順番で、AとBの分かれ方の明確さが違っています。
なお、標準化と正規化で、標準化の方が比率が大きいのは、Bに比べてAのサンプル数が極端に少ないためと考えられます。
主成分分析の後に標準化や正規化をすると効果的なのは、主成分分析によって、AとBの違いという特徴と、AもBも一直線に並んでいるという特徴が、それぞれ、ひとつの変数に表れるようになっていることが理由のようです。 こうなることで、ひとつの変数ごとに標準化や正規化をする処理が効果的に働いたと考えられます。
左が標準化（Standardization）の後に主成分分析（PCA）、右が正規化（Normalization）の後に主成分分析（PCA）です。
標準化、正規化、主成分分析を単独で実施した時と、結果が変わらないです。 組合せる時は、順番が大事なことがわかります。
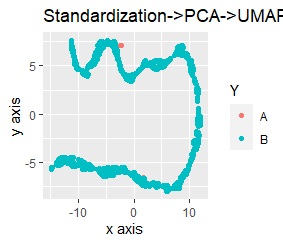
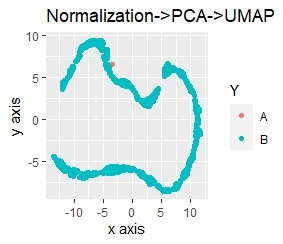
UMAPをする前の、前処理だけの結果は下図になっています。 PCAだけの時と変わらないです。
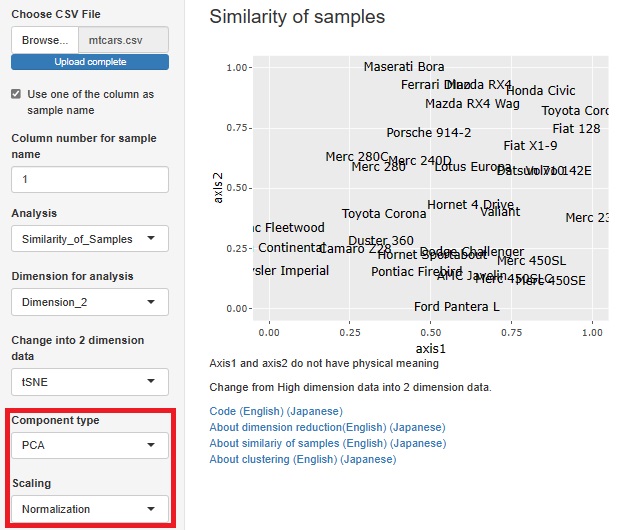
R-EDA1
では、
高次元を２次元に圧縮して可視化
の方法を使う時に、上記の方法を単独や、組合せて使えるようにしてあります。
組み合わせた場合は、主成分分析が先に処理されます。
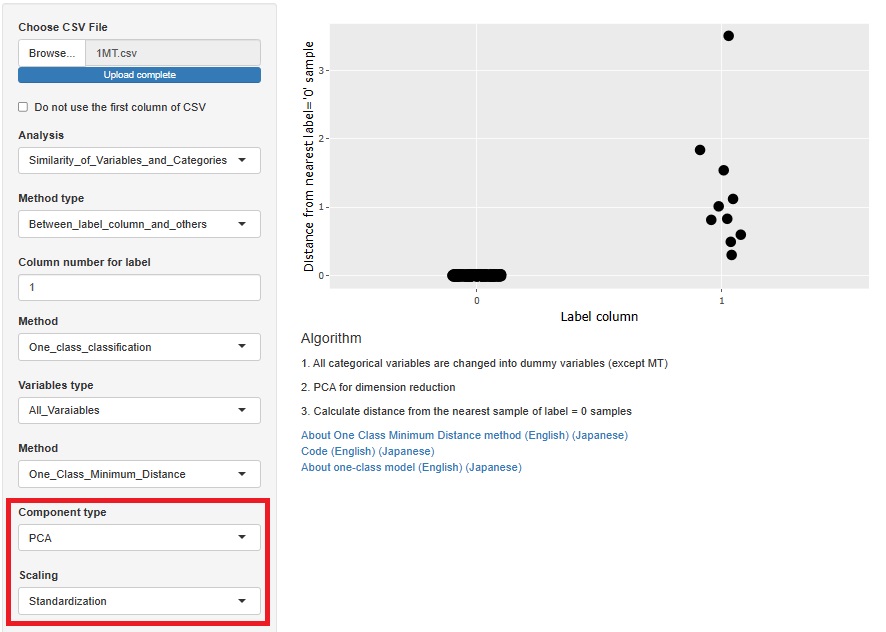
1クラス最小距離法
でも、組合せられます。
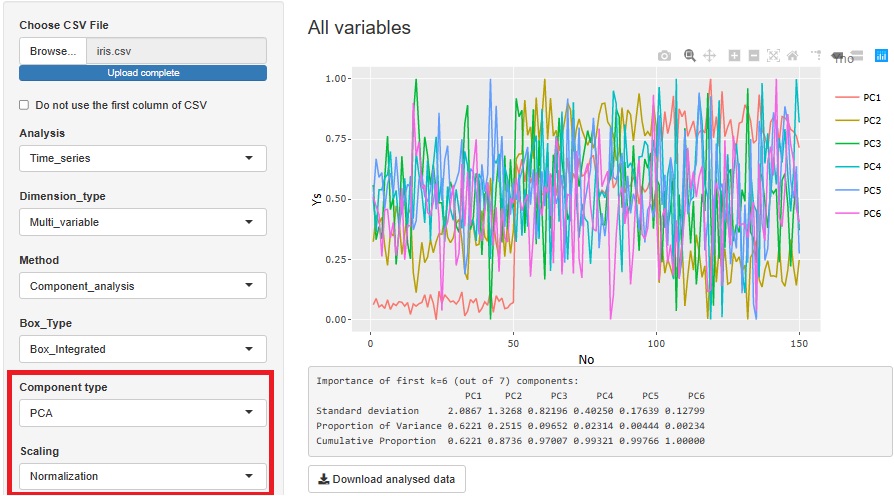
時系列解析
でも、組合せられます。
時系列解析
では、主成分分析（PCA）だけでなく、
独立成分分析（ICA）や
因子分析（Factor_analysis）とも組合せられます。
順路
次は
中間層を使った解析
