トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

1クラス最小距離法

1クラス最小距離法は、 主成分MT法 と 近傍法 の、いいとこどりになっています。

この方法の出力は、 単位空間 のサンプルの一番近いものとの距離です。 単位空間 の個々のサンプルについて、最近傍のサンプルとの距離を見ます。 それらの距離の分布や最大値と、信号空間の個々のサンプルについて、単位空間のサンプルで一番近いものとの距離を見比べることで、 異常性を判断できるようにしてあります。

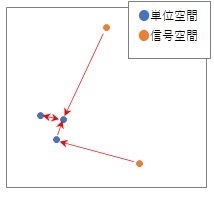
MT法 をベースにした方法と違って、単位空間の分布の中心を使わないので、中心が２個以上あったり、中心のようなものがなくても使えます。

弱点として、すべての組合せについて、サンプル間の距離を計算するため、 単位空間のデータが多過ぎると、計算時間が非常に長かったり、 メモリが足らなくて計算できなくなる可能性があります。 その場合は、分布の範囲は変わらないようにしながら、適度に間引く必要があります。

LOF （近傍法の一種）よりも良い点としては、異常値が複数あってそれらが近い時に、正常値と間違わないようになっている点があります。 計算時間を弱点として挙げましたが、LOFと比べれば、相当速いです。

なお、「1クラス最小距離法」は筆者が考えた方法です。 名前も筆者がつけたものです。 シンプルな方法なので、すでに世の中に同じものがあっても、おかしくないと思っていますが、今のところ、筆者は知りません。 同じものがあれば、名前はそちらに合わせるつもりでいます。

一般的な最小距離法との違い

距離が最小のものや、最小だけでなく２番目、３番目等も扱う方法は、サンプルの類似度を調べる方法として、一般的によく知られています。 クラスター分析 にもあります。

１クラス最小距離法と、これらの方法の違いは、距離を調べる相手のサンプルを 事前に「基準（ 単位空間 ）」と決めたサンプルに限定している点にあります。

Rを使った実施例

Rによる異常の近傍法分析 のページには、1クラス最小距離法の実施例があります。

多重共線性 のあるようなデータの時にでも、思ったような結果を出す目的と、計算量を少しでも減らす目的で、 主成分分析 をデータの前処理に入れています。 また、寄与率の低い主成分に重要な情報が入っていても、見落とさないようにするために、「主成分の 標準化 」という、普通は使われない手順が入っています。

順路 次は 数量化理論