MT法で計算がおかしい時 のようにして、 多重共線性 がある時に、データの意味を考える事は、とても大事です。 しかし、その辺りはあまり気にしないことにして、 とにかく異常の判定をできる仕組みを作りたい事もあります。
そのような場合は、データの前処理として、 主成分分析 を使う手があります。 主成分をMT法の入力データにします。
MT法をする場合、逆行列の計算があるため、
単位空間
のデータは
「変数の数 ＜ サンプル数」
になっている必要があります。
ところが、この計算をする前に主成分分析をしておくと、
「変数の数 ＞ サンプル数」
のデータを、
「変数の数 ＜ サンプル数」
のデータに変換する事ができます。
サンプル数が少ない時は、モデルの汎用性に不安があります。 しかし、そうは言っても、何も計算できないよりは、ある程度の手応えが得られた方が良い事は、多々あります。 主成分MT法には、この使い道もあります。
マルチ法は、 「変数の数 ＞ サンプル数」の状況や、 多重共線性 でも MT法 を使う方法として、作られています。
マルチ法では、まず、変数をいくつかのグループに分け、それらについてMDを計算します。 次に、ひとつのサンプルについて複数できたMDを中間変数として、中間変数のMDを計算して、全体を表すMDとします。
主成分MT法では、変数のまとめ方は、主成分分析の結果として自動的に決まります。 マルチ法では、変数のまとめ方は分析者が決める必要があります。 この点が、主成分MT法とマルチ法の違いになっています。
主成分MT法を異常の原因分析に使おうとする時の難しさですが、上の例の場合、「では、正常と異常の違いは何か」ということがわからないところになります。 こういう分析に進むのでしたら、主成分MT法ではなく、普通のMT法で変数を絞り込んで、絞り込んだ変数で散布図を作った方が、 その後の見通しが良いです。
MT法による異常の原因分析 のページは、そのような方法の説明になっています。
ただ、主成分MT法でないとできない分析もあります。 Rによる主成分回帰分析 に主成分回帰分析の場合の例がありますが、 隠れ変数 が原因になっている場合は、元の変数だけをいくら見ても正常と異常の違いはわからないため、主成分と変数の関係から、原因を考察する分析が必要になります。
MT法でMDが計算できない事の対策として、いくつかの方法が考案されています。 ただ、筆者の知る限りでは、決定版のようなものはないようです。
このページの主成分MT法は、筆者が付けた名前です。 主成分回帰分析 というものがありますので、それと同じように名前を付けました。
なお、主成分MT法は、 MT法 の発展版という流れのため、上記の計算例では、 マハラノビスの距離 を使っています。
しかし、主成分同士は相関がありませんので、マハラノビスの距離を使う利点が半減しています。 さらに、標準化された主成分を使う場合、マハラノビスの距離とユークリッドの距離は同じになりますので、 わざわざマハラノビスの距離の計算をする必要はなくなります。
RによるMT法 のページで、主成分MT法もあります。
R-EDA1
では、主成分MT法ができるようになっています。
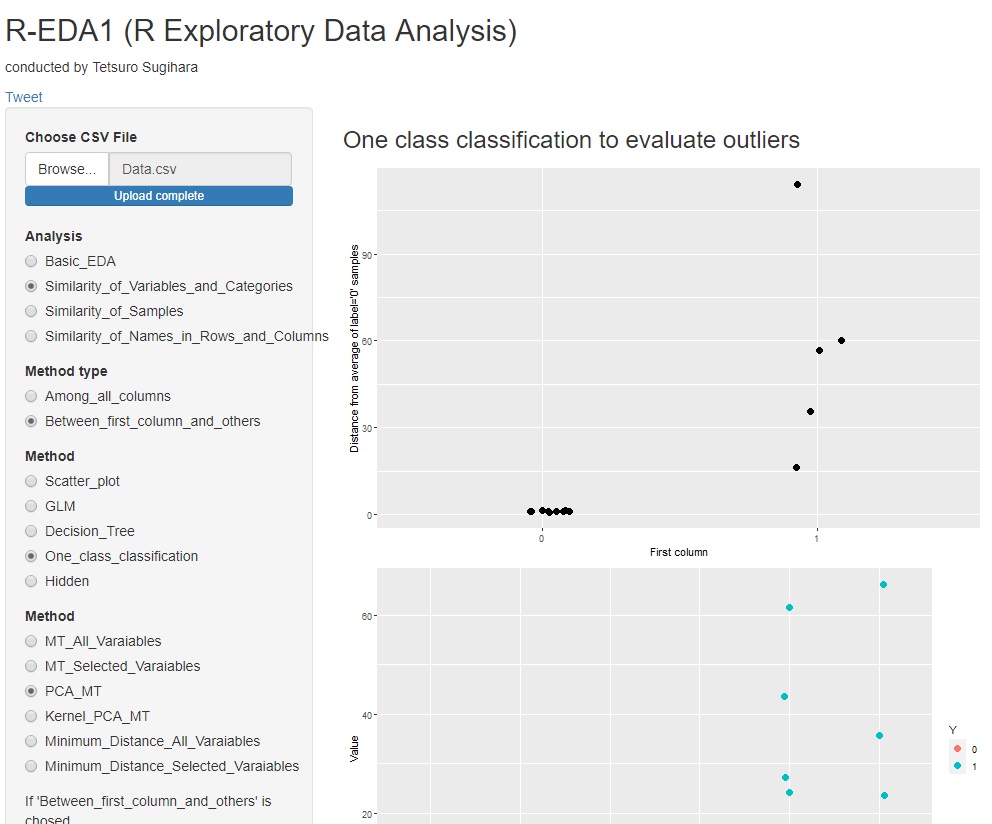
標準化主成分得点の２乗和は、マハラノビス距離の２乗和と一致する性質も利用できるようになっています。 主成分ごとに、標準化主成分得点の２乗が計算されたグラフも作られますので、どの主成分がラベルの違いに影響しているのかがわかります。
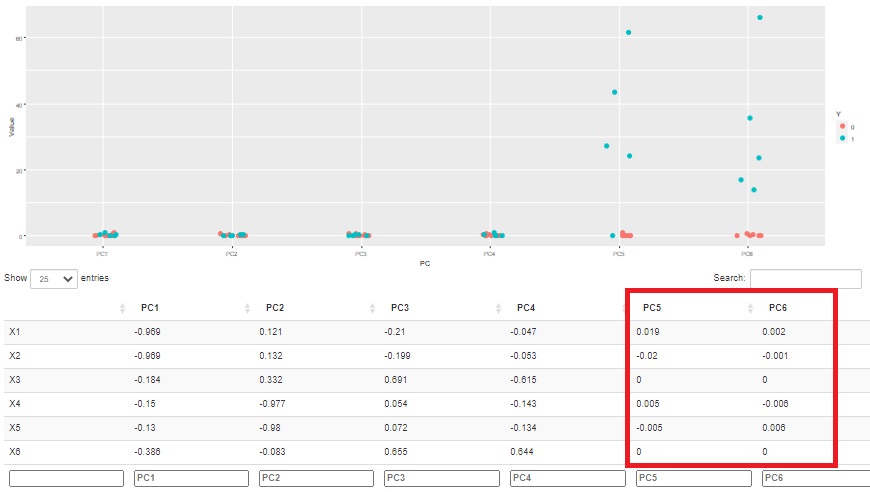
また、主成分と元の変数の相関係数もわかるようにしているので、元の変数との関係も調べられます。 下図の例だと、PC5とPC6という２つの主成分が正常と異常の違いに影響していることがわかります。
さらに、この例の場合、PC5とPC6は、元のデータのどの変数とも相関が低いことがわかります。
つまり、元のデータで、普段見えている増減とは異なることが、正常と異常に影響していることがわかります。
「アンスコム的な数値例で学ぶ統計的方法23講」 廣野元久・永田靖 著 日科技連 2013
統計的な方法について、一般的な解説書にはない話をしている本です。MT法もそのひとつです。
マハラノビス距離でわかった外れ値の外れの理由の解析は、変数毎ではなく、主成分分析でしています。
標準化主成分得点の２乗和は、マハラノビス距離の２乗和と一致するそうです。
つまり、マハラノビス距離は、主成分で分析できます。
「品質を獲得する技術」 宮川雅巳 著 日科技連 2000
マハラノビス距離の平方和（２乗和）は、主成分得点の２乗を固有値の逆数で重み付けされた和として、
主成分分析との関係を示しています。
「よくわかるMTシステム ：品質工学によるパターン認識の新技術」 田村希志臣 著 日本規格協会 2009
「変数の数 ＞ サンプル数」の時や、多重共線性がある時にMT法が使えない時の方法として、
マルチMT法を紹介しています。
マルチMT法がとても詳しく書かれています。
「入門 MTシステム」 立林和夫 著 日科技連 2008
マルチ法が、少し紹介されています。
「おはなしMT（マハラノビス・タグチ）システム」 鴨下隆志・矢野耕也・高田圭・高橋和仁 著 日本規格協会 2004
マルチ法が、少し紹介されています。
順路
次は
カーネル主成分MT法
