MT法 や 主成分MT法 は、正規分布を前提にした理論なので、データに合わない事があります。
主成分分析には、非正規分布のための理論として、 カーネル法 を使うカーネル主成分分析があります。
そこで、カーネル主成分分析をMT法の前処理にした「カーネル主成分分析」という方法も、理論としては作れます。
カーネル主成分分析には、 One-Class SVM の長所を持ったような理論として、使える可能性があります。 ただ、この方法には One-Class SVM と同じようにカーネル関数の調整がいるので、同じ難しさがあります。
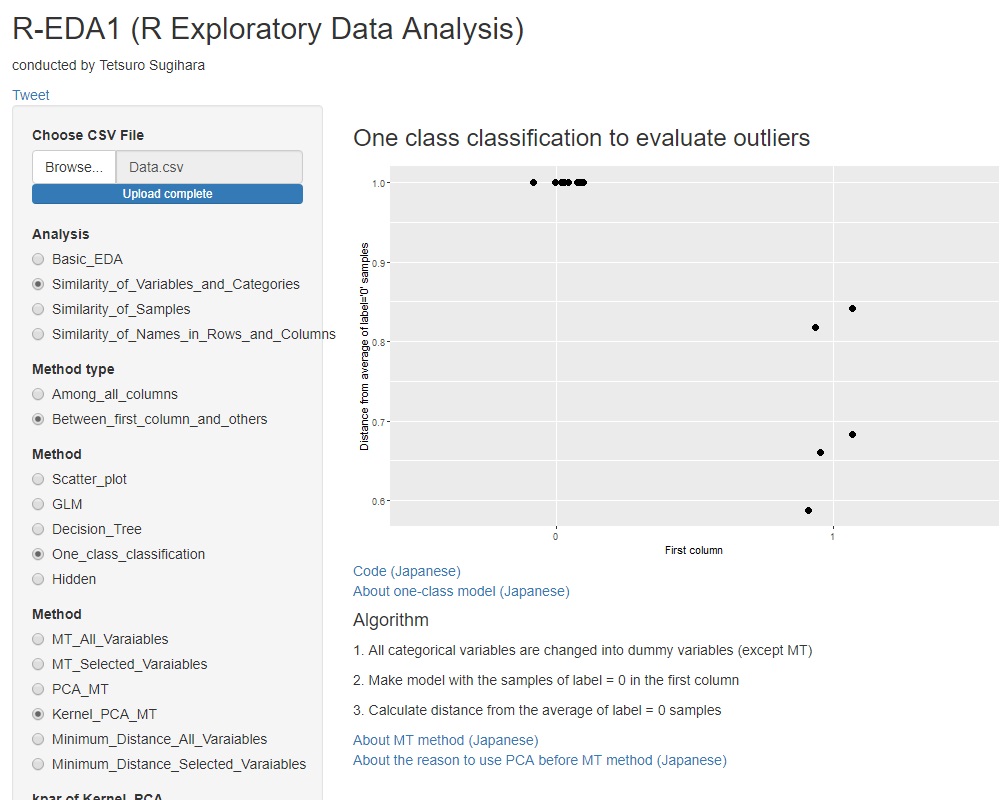
カーネル主成分分析を使うと、下図のようなグラフになることが多いようです。
単位空間（グラフでは「０」のラベル）のマハラノビス距離がほぼ１になります。 MT法では、マハラノビス距離を次元数で割った値を、「マハラノビス距離」と呼びますので、平均が１になるの想定通りです。 平均が１になるのは良いのですが、ばらつきが非常に小さいです。
カーネル主成分MT法のもうひとつの特徴として、カーネルの選び方によっては、 信号空間（グラフでは「１」のラベル）のマハラノビス距離が、すべてのサンプルで、１よりも小さくなります。 パラメタの選び方によっては、すべてほぼ０になることもあります。 普通のMT法をすると、１よりも大きな値になることがほとんどなのですが、データの表れ方が逆になっています。
筆者自身はカーネル主成分分析の数理をきちんと確認できていないのですが、 起きていることから考えると、rbfdotをカーネルにすると、学習用のデータを多次元の超球面の球面上に配置するようにモデルが作られるようです。 すべて球面上なので、データの中心（平均値）からの距離が、皆同じで１になるようです。
そのようなモデルに対して、学習データとは異なる値のデータを入れた場合、それらは超球面の内側に計算されるようです。 うまくモデルを作ると、学習データから外れているデータは、すべて距離が０の原点に配置されるような計算になるようです。
マハラノビス距離が１に近ければ学習データとほぼ同じで、少しでも異なると、０になるという性質は、場合によっては便利な性質かもしれません。
Rの実施例は、 RによるMT法 のページにあります。
R-EDA1 でも、カーネル主成分MT法はできるようになっています。 カーネル関数は４つ選べます。
カーネル主成分分析は、下記の金明哲先生のページを参考にさせていただきました。
http://mjin.doshisha.ac.jp/R/Chap_31/31.html
順路
次は
混合分布MT法
