MT法 を勉強すると、「異常の状態を数理で表現できるみたいだから、異常の原因分析（ 因果推論 ）に使える！」と思いたくなります。（筆者自身はそうでした。）
そこで、 MT法の手順 を進めて、 マハラノビスの距離 を計算するのですが、「この後どうすれば、異常の原因がわかるのか？」と行き詰まります。
このページはこんな状況の話です。
世の中の多くの問題は、１変数だけで異常がわかるものが多いと思います。 １変数だけでわかるような異常は、「正常時の最大値と最小値より外側」や、「３σ」と言った方法が使えますので、MT法を使う必要がないです。
MT法が価値を発揮するのは、２変数以上の場合です。
ところで、MT法の計算は、変数が100個くらいあってもできるのですが、 現実の問題で、100個の変数が複雑に動くような異常現象には出会わないです。 せいぜい２、３個で決まっています。 筆者の経験の話にはなるのですが、それらの２、３個と似たような変数が、他にもたくさんあるような状態が、一番多いです。
話はそれますが、これが原因で 多重共線性 で悩むことになります。
MT法でやりたいことは、２、３個の変数の組合せを抽出する作業になります。
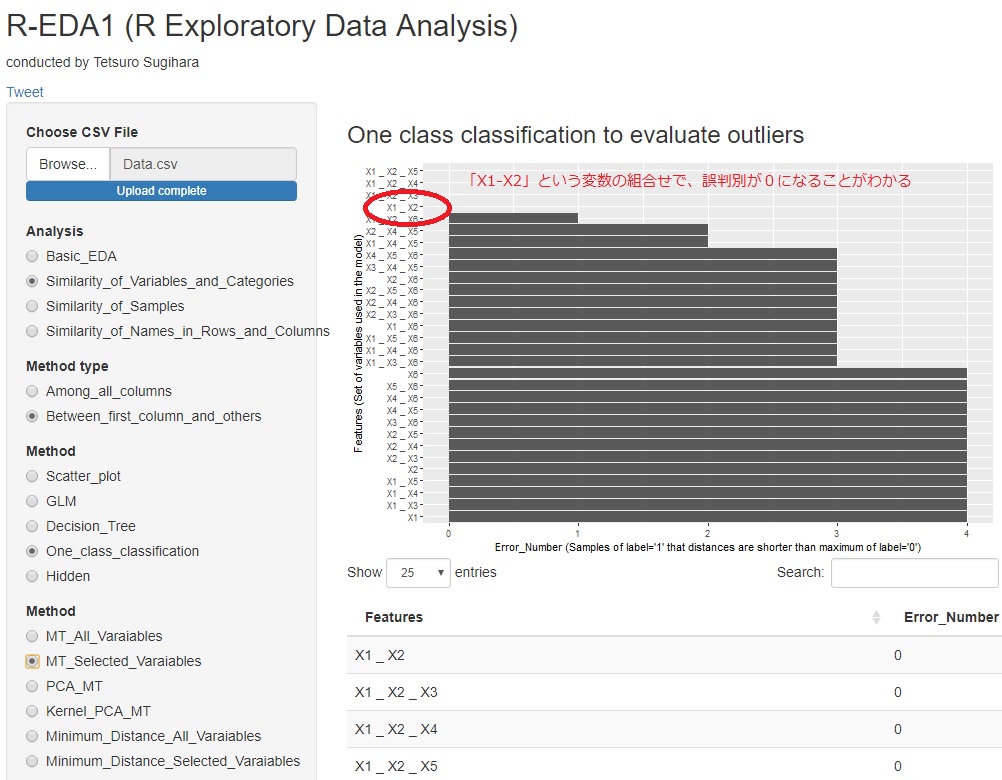
R-EDA1 では、１〜３個の変数のすべての組合せについて、単位空間でマハラノビス距離が最大になるサンプルのマハラノビス距離と、 信号空間のサンプルのマハラノビス距離を比べるアルゴリズムを使っています。
少数の変数のモデルの候補がたくさん抽出されますので、そこからはデータの背景の考察になります。
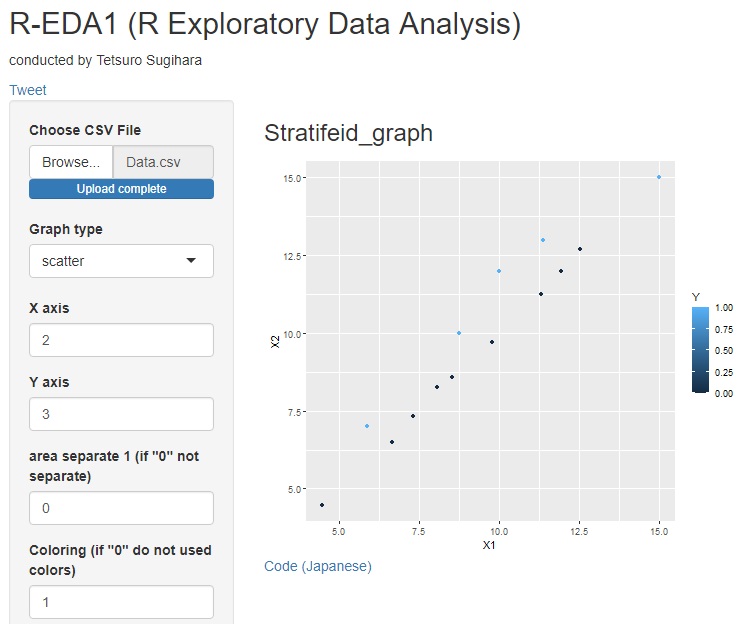
X1とX2という変数で散布図を作ると、ラベルが０（黒）とラベルが１（青）では、データの並び方が違うことがわかります。
ちなみに、こういう種類の異常を分析できるのが、MT法の特長になります。
世の中のMT法の解説では、すべての変数について、「モデルに入れる、入れない」の２水準にして、 実験計画法を使って、水準を入れた時の効果を調べる方法が紹介されていることがあります。
順路
次は
手法による得意な分布の違い
