重回帰分析 が役に立つ場面では、上のようなデータになっていることが、よくあります。
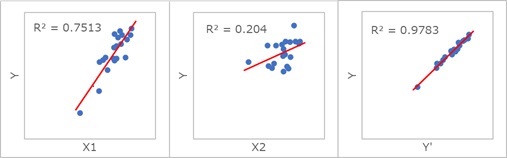
重回帰分析
が役に立つ場面では、上のようなデータになっていることが、よくあります。
上の例では、X1、X2という説明変数があり、Yという目的変数があります。 グラフは、一番左が、X1とYの関係、真ん中がが、X2とYの関係を表しています。 一番右が重回帰分析のモデルで求めた、Y'という予測値とYの関係を表しています。
X1とX2の片方だけでもYとの相関は見られますが、重回帰分析のモデルだと、さらに強い相関になっています。
下の例の場合、X1、X2の片方だけだと、Yとはまったく相関が見られません。
しかし、重回帰分析のモデルだと、強い相関が見られます。
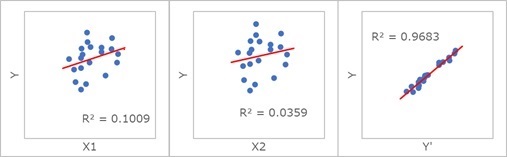
このサイトで「隠れ変数」と呼んでいるのは、このような現象です。
「隠れ変数」というのはこのサイトの造語です。 隠れ変数は、 因子分析 で言うところの「潜在変数」の一種です。
因子分析では、潜在変数がいくつかあって、それがデータとして得られている変数の背後にあると考えます。
ここでいう隠れ変数というのは、 データとして得られている変数を見た時に、例えば、潜在変数がひとつあることは容易に推定できるものの、 実はもうひとつある時に、もうひとつの方は推定できない状況の時の、推定できない方の潜在変数のことです。
隠れ変数があれば、上の例の場合は、下図のようになります。 このグラフは、横軸が原因系と考えている変数で縦軸がYです。
この図を見ると、YとPC2という変数はとても相関が高いことがわかります。
PC2が隠れ変数です。
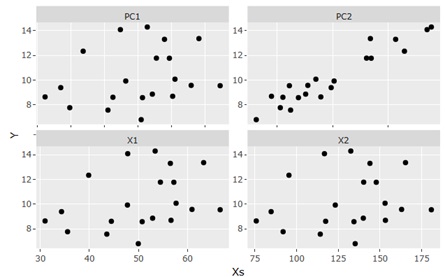
隠れ変数が見つかるのは、X1やX2という変数が、２つの変数が合成されたものになっている場合です。
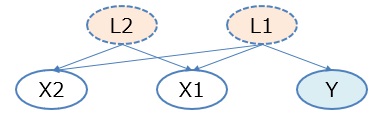
隠れ変数が見えないのは、X1やX2を見ている時に見えているのは、合成した変数の片方だけになっているためです。
例えば、X1の数値が「10」で、
10 = 9 + 1
という計算の結果、この数値ができているのなら、「9」の方の変数の方が見えているもので、「1」の方の変数は見えません。
隠れ変数が隠れていたのは、小さな影響しかないように、合成されていたためになります。
隠れ変数が見つかると「見つかった！」となりますが、その後のデータ分析は、なかなか難しいです。
Y、X1、X2と違って、隠れ変数は実際に測定して得られたものではなく、計算上、存在が推測される変数なためです。
「X1とX2に合成されて含まれて来るような要因は、実際には何があるのか？」、といったように、 メタ知識 を駆使する必要があります。
上記は、隠れ変数が見つかった場合ですが、上記の例は、 主成分分析 を使って、隠れ変数を見つけています。
独立成分分析 や 因子分析 でも見つけることができます。 どれが適しているかは、データの構造によるようです。 （分解分析の違い）
上記の例では、目的変数Yは分けてから、説明変数Xだけで、主成分分析をしています。
その後で、Yと主成分の関係を見ています。
Yの変数を分けずに、主成分分析などをしても、Yと共通になる成分を探すアプローチもできます。
この方法は、結局のところ、 疑似相関からの因果推論 と同じになります。 疑似相関からの因果推論 では、「疑似相関」と言っているくらいなので、YとXに相関関係が見えているようなデータがスタートになり、 隠れ変数の探索の時は、YとXには、相関関係が見えないようなデータがスタートになるところが違いますが、潜在変数をあぶり出そうとするところが同じなので、方法が同じになります。
隠れ変数のような変数があったとしても、いつでも抽出できる訳ではないです。
まず、X1やX2に含まれる割合があまり小さ過ぎると、隠れ過ぎていて見えないです。
また、X1やX2への含まれる割合が同じ場合も、見つかりにくくなります。
下記の方法は、「目的変数を分ける方法」です。 「目的変数を分けない方法」は、YとXを区別しないで、普通に因子分析や、独立成分分析をすればできます。
R-EDA1 でもできます。
主成分分析、独立成分分析、因子分析を選べます。
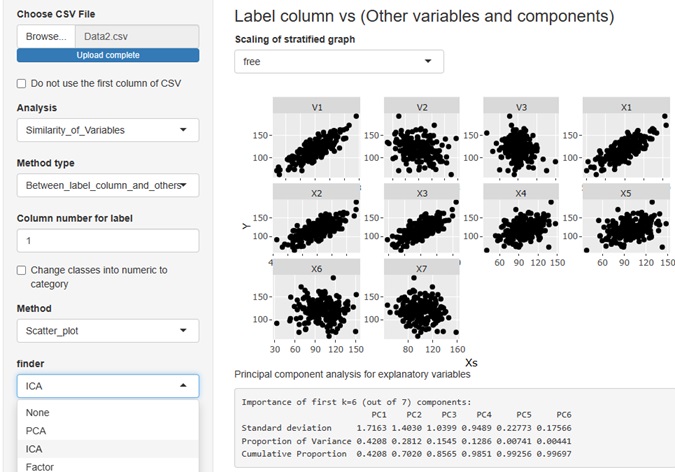
上の例は、独立成分分析を選んだ場合です。 散布図の縦軸は、すべて目的変数のYです。 横軸のV1,V2,V3,V4が独立成分で、X1,X2,X3,等が、元データの説明変数です。
Rによる実施例としては、 Rによる隠れ変数の分析 のページがあります。
Pythonによる実施例としては、 Pythonによる隠れ変数の分析 のページがあります。
順路
次は
主成分回帰分析による因果推論
