このページのタイトルは、 主成分回帰分析 ですが、 独立成分回帰分析と因子回帰分析 も含めた話です。
重回帰分析 の一般的な解説では、精度の高いモデルを作ることを目的としていることが多いです。 変数の選択 は、そのためにします。
多重共線性 や 過学習 を避ける目的でも 変数の選択 は大事です。
変数の選択によって、一番良いと考えられるモデルができます。
ところが、筆者の経験の場合にはなりますが、因果推論を目的として重回帰分析をする時は、一番良いモデルになる変数を選ぶことには、あまり意味のないことが多いです。
因果推論をしたい場面は、実験データではなく、ありもののデータから何とかしたいことが多いです。 そのようなデータは、「見つけたい因果関係のヒントになればラッキー」くらいのデータで、原因そのものを表していないことが普通です。 変数の選択によって選ばれた変数について、「原因の可能性が高い」という考察を進めると、失敗することがあります。
そのようなデータの中から、一番良いモデルになる変数を選ぶのは、考察のヒントにはなりますが、それ以上には進みにくいです。 むしろ、一番良いモデルになる変数と多重共線性の関係のある変数があるのなら、それらがどんなものかをセットとして把握した方が、 因果関係を突き止めるヒントになることがあります。
主成分回帰分析についての一般的な説明では、サンプル数が変数の数よりも少なくても、重回帰分析のモデルが作れる点や、ロバストなモデルを作る点が説明されることが多いようです。
因果推論を目的としている時は、説明変数がグループ単位で考察できるようになるところが、主成分回帰分析の良いところになります。 これによって、 潜在事実の探索 が進めやすくなります。
スパースモデリング の思想に「オッカムの剃刀（かみそり）」と呼ばれるものがありますが、因果推論を目的とするのなら、単純な変数の選択でシンプルなモデルを作るのではなく、潜在変数でシンプルなモデルを作る方が、見通しがよくなります。
単回帰分析の結果と同じ時と違う時 のページにあるように、 隠れ変数が目的変数と相関が高いデータに対して、 重回帰分析 をした場合、隠れ変数ではない変数の存在がうまく消えて、隠れ変数の存在が表れるように、 各変数を差し引きして、線形和が作られます。 このようにして、説明変数の線形和と目的変数の相関が高くなります。
このため、一般的な重回帰分析で、このようなケースを分析すると、 「非常に精度の高いモデルが作れたが、線形和の係数がこうなった理由が考察できないので、説明変数との因果関係はわからない。」となります。 線形和の係数を丁寧に見て行くと、 「隠れ変数ではない変数の存在がうまく消えて、隠れ変数の存在が表れるように、 各変数を差し引きされた。」と読み取れなくもないのですが、 「係数を丁寧に見ればわかる」というのは、データ分析が得意ではない人に共感してもらいにくい進め方になります。
主成分回帰分析をすると、主成分という形で、隠れ変数の存在があぶり出されてくるので、見通しがよくなります。
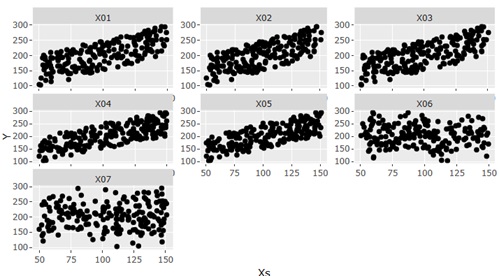
主成分回帰分析の例です。 下のグラフで、左側が分析用のデータで、右側が分析結果です。
元のデータが、YとXのグループです。
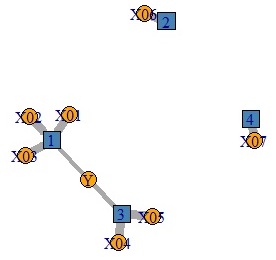
青い四角で数字が書いてあるのは、独立成分分析で抽出した成分です。
この分析は、Yが目的変数なのですが、Yと関係があるのは、1と3の２つの独立成分で、独立成分のそれぞれにXが結びついていることがわかります。
順路
次は
潜在変数モデルの使い分け
