トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

単回帰分析の結果と同じ時と違う時

「Yが１個で、Xが複数だから 重回帰分析 を使おう。」ということで、重回帰分析を使ってみても、 出せる結果が、 単回帰分析 と変わらないことは、よくあります。

単回帰分析の結果と同じ時と違う時は、どんな時なのかを知っていると、 結果の見方や見せ方の役に立ちます。

単回帰分析と重回帰分析で、結果が同じ時

下の図の見方ですが、Yが目的変数、X1、X2が説明変数です。 F1、F2というのは、 因子分析 で潜在変数と呼ばれているもので、データとしては持っていないけれども、そのデータの増減の原因になっている因子です。

Xの因子が共通の時

因果関係としては、X1とYに因果関係があり、X2とYにはなかったとしても、X1とX2の因子が共通の場合です。

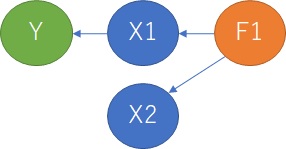
この場合、単回帰分析では、X1とYの相関が高くなるだけでなく、X2とYの相関も高くなることがあり、 本当の因果関係が、どちらにあるのかは、データだけでは判断することが難しいです。 相関係数の大きさで、どちらにあるのかを決めることはできますが、 「このデータだと、そうかもしれないが、いつもそうなるかはわからない」という疑念が残ります。

重回帰分析でも、 変数の選択 の方法を使って、X1とYだけを使ったモデルを作れるかもしれませんが、データによっては、X2とYのモデルが導かれるかもしれません。

XとYの因子が共通の時

擬似相関 がある場合です。

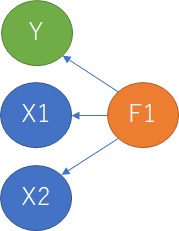
単回帰分析では、YとX01、YとX02の組合せのそれぞれについて、モデルが作れます。

重回帰分析でも、YとどのXを組み合わせても、あまり変わらないモデルになります。

単回帰分析と重回帰分析で、結果が違う時

２つのXの因子が、それぞれ異なる場合

２つのXの因子が、それぞれ異なり、YはXの線形和になっている場合です。

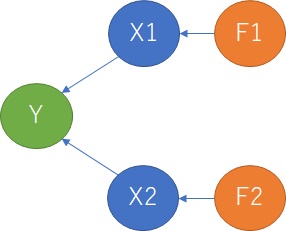
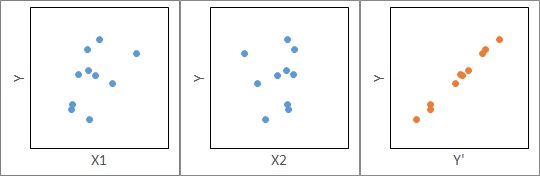
この場合、例えば、下図のようにX1とY、X2とYの組合せで散布図を見ると、いずれも相関があるようには見えないことがあります。

重回帰分析でモデルを作って、回帰式でYの推定値のY'を計算すると、YとY'には非常に高い相関が出て来ることがあります。

この場合は、単回帰分析だけだと、「YとXには関係がない」という結論になりますが、重回帰分析だと「YとXには関係がある」という結論になり、 現象のメカニズムの解明が進みます。

２つのXの因子のそれぞれが、２つの因子の影響を受けている場合

Xが２つで、因子が２つなのは、この前のケースと同じですが、それぞれのXは、F1とF2の線形和になっている場合です。 また、YはFの片方とだけ因果関係があるものの、Xとは因果関係がないです。

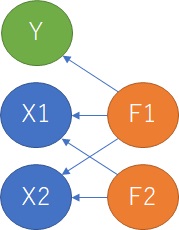
この場合も、X1とY、X2とYの組合せで散布図を見ると、いずれも相関があるようには見えないことがあります。 また、単回帰分析と重回帰分析で結論が異なる点も同じです。

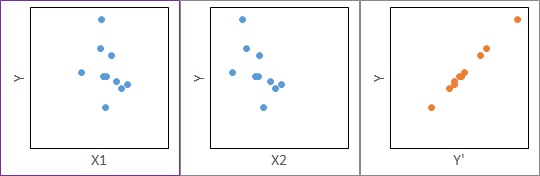
しかし、Xの背後にあるメカニズムが、「２つのXの因子が、それぞれ異なる場合」とは違います。

この場合、F1の影響がXに大きく出ていると、YとX1や、YとX2の相関は高く見えるようになるため、上記の疑似相関の場合とあまり変わらない分析になります。

考察が難しくなるのは、F1の影響がXに対して小さく、F1が 隠れ変数 になっている場合です。

この場合、重回帰分析の結果が、「２つのXの両方がYに影響している」となる点は、 「２つのXの因子が、それぞれ異なる場合」と同じです。 そのため、「２つのXの因子が、それぞれ異なる場合」のように解釈されやすいです。

「２つのXの因子のそれぞれが、２つの因子の影響を受けている場合」だと気が付くには、重回帰式の係数の値や符号を確認する必要があります。 「係数の絶対値が、ほぼ同じなのは、なぜ？」や、「この符号は、なぜマイナス？」ということで気付けることがあります。

F1の影響がXに対して小さい時は、係数を調整して、X1とX2に含まれているF2の影響を相殺させることで、Y’の中にF1の影響だけが残るような計算になります。 こうすることで、Y’とYの相関が高くなります。

順路 次は 多重共線性