疑似相関は、 相関係数で見えない事 のひとつです。
例えば、小学生の身長と、覚えている漢字の数の相関性は高いはずですが、 この結果を元にして、 「漢字をたくさん覚えれば、身長が伸びる。」とか、 「身長が伸びれば、漢字をたくさん覚えられる。」、という結論を出す方はいないと思います。 この場合は、「年齢と身長には相関があるし、年齢と漢字の数には相関があるだろうから、 身長と漢字の数にも相関があるように見えるのだろう。」、という理由が考えられます。
この例のような相関を「擬似相関」や「擬相関」と言います。
下図では、XとZ、YとZのような関係があった時に、XとYのデータが直線的に並んでいます。
XとYに直接的な関係がなくても、XとZ、YとZの関係によって、直線的にデータが並ぶようになっています。
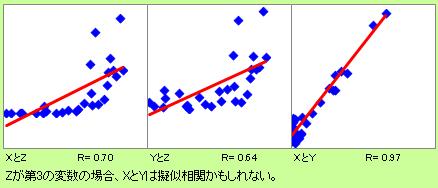
擬似相関の考察は、難しいです。 第３の変数をデータで持っていれば、少しは調べようがありますが、 それでも、XとYに因果関係があるのかどうかは、統計学の知識だけではわかりません。
身長と漢字と年齢の関係を例にしてみましたが、 この場合は、「第３の変数は年齢」だと、常識で判断できます。 しかし、高度な技術や、未知の現象の話になってくると、どれが第３の変数なのかは、データだけでは見当が付きません。
第３の変数のデータを持っていない事もあります。 一番深刻なのは、第３の変数のデータがないだけでなく、それが何かもわかっていないケースですが、こうしたケースが一番多いかもしれません。
擬似相関の関係になっている２つの変数について、共通している事を考察すると、それらの変数が増減する理由がわかる事があります。
因果関係をデータ解析で調べたい時には、擬似相関はこんな風に利用します。 擬似相関は、解析の段階を次に進める突破口になる事があります。
擬似相関を考慮した相関係数として、 偏相関係数 が考案されています。
ただし、これは第３の変数を持っていないと使えません。
順路
次は
擬似相関を使ったデータ分析
