 僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
 僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
媅帡憡娭偺儁乕僕偵偁傞傛偆偵丄 乽媈帡憡娭偲偄偆傕偺偑偁傞偐傜丄憡娭娭學偲場壥娭學偼摨偠偱偼側偄丅乿偲偄偆偺偼丄傛偔尵傢傟傞榖偱偡丅 媈帡憡娭偼丄僱僈僥傿僽側僀儊乕僕偱岅傜傟傞偙偲偑懡偄偱偡丅
偙偺儁乕僕偼丄媈帡憡娭偑偁傞偙偲傪慜採偵偟偨僨乕僞暘愅偱偡丅 媅帡憡娭傪丄愊嬌揑偵巊偆曽朄偱偡丅
壓婰偺乽堘偆忦審偺Y摨巑傪挷傋傞乿偲乽梊應惛搙偺敾掕乿偱偼丄媈帡憡娭偺娭學偺偁傞僨乕僞偑丄捈慄揑偵僨乕僞偑暲傇惈幙傪巊偄傑偡丅
墶幉偑A偺棙塿丄廲幉偑B偺棙塿偲偟傑偡丅
偙偺帪丄惓偺憡娭偑偁傟偽丄椉摼偺娭學乮僂傿儞僂傿儞丗Win-win乯傪昞偟偰偄傑偡丅
晧偺憡娭偑偁傟偽丄擇棩攚斀偺娭學乮僩儗乕僪僆僼丗Trade-off乯偺娭學傪昞偟傑偡丅
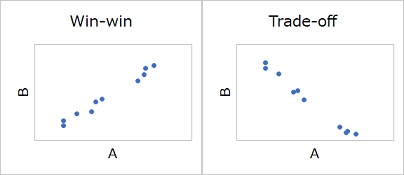
偙偺応崌偼乽X傪屌掕偟偨帪偺Y傪挷傋傞丅乿偲偄偆尵偄曽傕偝傟傑偡丅
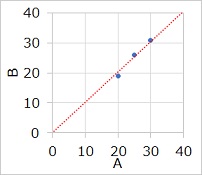
椺偊偽丄0暘丄10暘丄20暘偺壏搙偑丄偁傞壏搙寁偱20亷丄25亷丄30亷丄
暿偺壏搙寁偱19亷丄26亷丄31亷偩偭偨偲偟偰丄
乮20丄19乯丄乮25丄26乯丄乮30丄31乯偺抣傪僾儘僢僩偟偰丄
俀偮偺壏搙寁偺娭學傪挷傋傞応崌偑偁傝傑偡丅
偙偺応崌丄帪娫偑X偱偡偑丄X偺抣偑僾儘僢僩偺拞偵偼擖偭偰偒傑偣傫丅
Y摨巑偺娭學偺傒傪尒偰偄傑偡丅
偙偺椺偱偼X偑検揑側僨乕僞偱偡偑丄
椺偊偽丄X偑搶嫗丄暉搰丄怴妰偺傛偆側幙揑僨乕僞偱傕丄偙偺曽朄偼巊偊傑偡丅
偙偺峫偊曽偼丄 昳幙岺妛 偺 昗弨SN斾 偱墳梡偝傟偰偄傑偡丅
偪側傒偵丄乮0暘丄20亷乯丄乮10暘丄25亷乯丄乮20暘丄30亷乯傪僾儘僢僩偟偰丄 帪娫偲壏搙偺娭學傪挷傋傞応崌偑丄嘆偺巊偄曽偱偡丅 嘆偺巊偄曽傪丄俀偮偺壏搙寁偱峴偭偰丄 椉曽偺X偲Y偺憡娭學悢傪斾妑偡傞曽朄傕偁傝傑偡丅
擇廳應掕乮懳墳偺偁傞僨乕僞乯 偼丄偙偺曽朄偲帡偰偄傑偡丅
梊應幃傪嶌傞帪偵巊偭偨X偺抣傪幃偵擖傟偰丄Y傪寁嶼偡傞偲丄 梊應抣偺Y乮寁嶼偟偨Y乯偲丄幚應抣偺Y乮梊應幃傪嶌傞帪偵巊偭偨Y乯偺2偮偑梡堄偱偒傑偡丅 梊應幃偑揔愗偱偁傟偽丄 梊應抣偲幚應抣偑捈慄忬偵暲傇偼偢偱偡丅 偦偙偱丄梊應惛搙乮僼傿僢僥傿儞僌乯偺敾掕傪憡娭學悢偱偡傞偙偲偑偱偒傑偡丅
偙偺昡壙偵巊偆憡娭學悢偼丄 廳憡娭學悢偲傕屇偽傟傑偡丅
偙偺娭學傪挷傋傞応崌偼丄憡娭學悢偺俀忔偺丄乽寛掕學悢乿偺曽偑懡偔巊傢傟偰偄傑偡丅 寛掕學悢偺応崌偼丄亾傪扨埵偵偡傞偙偲偑偁傝傑偡丅 寛掕學悢偼丄乽寛掕棪乿傗丄乽婑梌棪乿偲尵傢傟傞偙偲傕偁傝傑偡丅
寛掕學悢偺媮傔曽偵偼丄乽憡娭學悢傪寁嶼偟偰偐傜俀忔偡傞曽朄乿偲丄 乽梊應抣偲幚應抣偺丄偦傟偧傟偺暘嶶傪媮傔偰偐傜丄偦傟傜傪妱傝嶼偡傞曽朄乿偺俀偮偑偁傝傑偡丅 媮傑傞抣偼摨偠偱偡丅
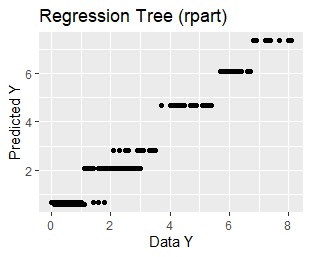
夞婣暘愅 摍傪梊應偵巊偆応崌偼丄幚應抣偺X偲Y偺憡娭惈偺昡壙偲丄 Y'乮梊應抣乯偲Y乮幚應抣乯偺憡娭惈偺昡壙偑偁傝傑偡丅 Y'偼丄X偺幚應抣傪梊應幃偵戙擖偡傞偲丄媮傔傞偙偲偑偱偒傑偡丅
壓恾偼丄
儌僨儖栘
偺儁乕僕偵偁傞椺偱偡丅
弴楬


 師偼
憡娭偺専掕
師偼
憡娭偺専掕

